統計学：初学者向けにPythonによる確率分布の取り扱いを基本から解説

この記事はこんな方におススメです

データを分析をしたいが、どこから始めてよいかわからない方
データを仕事に活かしたいが、データの解釈の仕方がわからない方
統計学を体系的に学んだことがない、初学者の方

▶ 初学者向けに統計学を基本から解説しています。はじめから学びたい方は以下の記事からどうぞ

統計学を学んだことがない初学者を対象にして、基礎から解説していきます。第一回目は記述統計を扱います。記述統計では代表値と散布度の取り扱いに分けて解説していきます。この投稿を最後まで読むと記述統計とは何かがわかり、実際にPythonでコードをかけるようになります。

はじめに

統計学を学んだことがない初学者を対象にして基礎から解説しています。今回は確率分布を扱います。確率変数、確率分布の順に解説し、最後にPythonによる実装をおこないます。この投稿を最後まで読むと確率分布とは何かがわかり、実際にPythonでコードをかけるようになります。

確率分布

確率変数

まずは確率変数から確認していきましょう。確率変数とは値が確率的に変動する変数のことです。確率変数はXで、確率変数のある値に対応する確率をP(X)と表します。高校の授業の導入時にはさいころの目などで学んだのではないでしょうか？

サイコロの目は１～６まであって、これらはそれぞれ確率的に変動します。なので、「サイコロの目」は確率変数といえます。各値は1/6の確率に対応していますね。

確率分布

確率分布は、確率がどのように分布をしているかを表したものです。連続変数の分布をみるときに、ヒストグラムを扱いました。これは、どの区間にどのくらいの値があるか、という「度数分布」を描画したものでした。「度数」ではなく「確率」がどのように分布しているかをあらわすのが、確率分布です。

▶　ヒストグラムに関して復習したい方は以下の記事をお読みください。

統計学：分布の描画方法を初学者向けに基本から解説します

統計学を学んだことがない方を対象に基本から解説しています。今回はデータを入手したらまず最初におこなう「分布」の確認についてです。分布を確認するにあたり、連続変数の場合とカテゴリ変数の場合に分けて、Pythonによる可視化の方法を基本から解説します。

度数分布では縦軸が度数、横軸がとりうる値の区間でした。これに対して、確率分布では、縦軸が確率、横軸がとりうる値（確率変数の各値）となります。

確率分布はたとえば、正規分布（norm）や一様分布（randint/uniform）、二項分布（binorm）、ポアソン分布（poisson）、指数分布（expon）などいろいろあります。サイコロの目であれば、１～６までの値が確率1/6となる「一様分布」ですね。

ところで、確率変数が離散型であるか、連続型であるかによって分布を表す関数が異なります。一様分布の場合、randint/uniformがありますが、これも確率変数が離散型か連続型かの違いによるものです。

離散型確率変数の分布を「離散型確率分布」、連続型確率変数の分布を「連続型確率分布」といいます。また、「離散型確率分布」を表す関数を「確率質量関数（PMF：Probability Mass Function）、「連続型確率分布」を表す関数を「確率密度関数（PDF：Probability Density Function）といいます。

確率変数が離散型のものを離散型確率変数、連続型のものを連続型確率変数という
離散型確率変数の分布を離散型確率分布、連続型確率変数の分布を連続型確率変数という
離散型確率分布を表す関数を「確率質量関数（PMF：Probability Mass Function）」という
連続型確率分布を表す関数を「確率密度関数（PDF：Probability Density Function）」という

Pythonによる実装

Pythonで確率分布を扱うときにはscipyライブラリのstatsモジュールを利用します。確率分布は以下の記述で得ることができます。これが基本構文となります。

stats.<確率分布>.<メソッド>
＜確率分布＞には、正規分布（norm）、一様分布（randint/uniform）、二項分布（binorm）、ポアソン分布（poisson）、指数分布（expon）などいろいろある

サイコロを振った時の出る目の確率分布をPythonで実装してみましょう。

確率分布

サイコロの目は一様分布でしたね。一様分布にはrandint()とuniform()があります。randint()は指定した数字の中でランダムな整数を生成する離散型確率分布を表す関数です。一方で、uniform()は指定した数字の間でランダムな値を生成する連続型確率分布を表す関数です。サイコロの目は離散型確率変数なので、randint()を使えばよいですね。

離散型確率分布

選んだ確率分布によって、準備されている＜メソッド＞は異なります。一例をあげると、確率分布から確率変量を取り出す場合は「rvs()」（rvs：random variates）、平均を求める場合は「mean()」、ぶ分散は「var()」、標準偏差は「std()」などです。

今回は離散型一様分布を表す関数なのでpmf()を使います。コードを書いていきましょう。

# ライブラリのインポート
from scipy import stats
import matplotlib.pyplot as plt
import japanize_matplotlib
%matplotlib inline

# 確率変数がとる値
x=np.arange(1,7)

# 確率質量関数
y=stats.randint(1,7).pmf(x)

# 描画
plt.plot(x,y,'o')
plt.vlines(x,0,y)
plt.grid()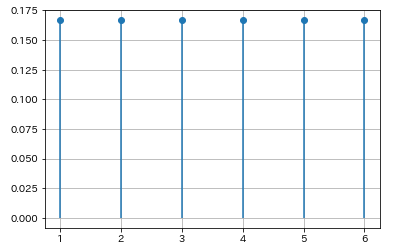

サイコロの目なのでrandint()では、rand(1,7)を指定します。その後、確率質量関数pmf()を指定して描画しています。簡単ですね。

連続型確率分布

次に、連続型確率分布をみていきましょう。連続型の一様分布はuniform()でしたね。uniform()では、位置と区間をloc,scaleで指定します。loc, scaleを指定すると区間[loc, loc+scale]で確率が一定になり、pdfにより出力される値は1/scaleとなります。やってみましょう。

# 確率変数がとる値
x=np.linspace(0,6,1000)

# 確率質量関数
y=stats.uniform(4,1).pdf(x)

# 描画
plt.plot(x,y,'-')
plt.grid()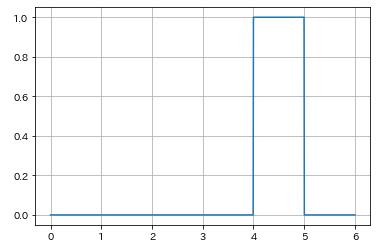

uniform(4,1)としたのでloc=4,scale=1なので、区間は[4,5]ですね。この区間で確率が1/scale=1で一定となります。

まとめ

今回は確率分布を扱いました。確率分には一様分布、二項分布、ポアソン分布など様々なものがあります。また、確率分布を関数であらわすときに、確率変数が離散型であるときは確率質量関数で、連続型であるときは確率密度関数であらわすのでしたね。最後に、Pythonでの実装方法を紹介しました。よく復習しておきましょう。