Python初心者向け：時系列データのモデルを基本から解説

▶ 時系列データ分析を基本から学びたい場合は、以下の記事も合わせてどうぞ。

今回は時系列データの取り扱いを基本から解説していきましょう。テーブルデータ的な取り扱いをすることもありますが、時系列データ特有の取り扱いがあります。まずは、時系列データの特徴の整理からはじめて、実際の処理の仕方を基本から解説していきます。

今回はStatsModelsを用いて時系列データの分析の仕方を学びましょう。まずは時系列データの周期性を確認する方法を基本から解説します。時系列データにはトレンド、周期変動、不規則変動の３つのパターンがあります。この３つの確認から始めましょう。

この記事はこんな方におススメです

時系列データの処理の仕方を知らない、または、基本から学びたい方
時系列データを扱ったことがあるが、体系的に整理できていないので学びなおしたい方

はじめに

前回に引き続き、時系列データを扱います。基本的に（弱）定常性が仮定されない、時系列解析を実施することができません。まずは、定常性の確認から始めましょう。非定常なデータは加工して定常なデータにしたうえで時系列解析を始めます。時系列解析のモデルにも様々なものがあります。今回は時系列解析のモデルの種類を整理しましょう。

定常性の確認

基本的に「（弱）定常性」が仮定されないと、時系列解析はできません。時系列データでは、定常性がないデータを分析してしまうと、見せかけの相関（疑似相関といいます）がおこってしまいます。

定常性とは、時間によらず期待値、自己共分散が一定である時系列データの性質でしたね。トレンド成分が含まれているものは、もちろん「非定常」なデータです。ある時系列データが定常であるかどうかを確認するための最も簡単な方法はプロットしてみることです。そして、

時間の経過によらず一定の値を軸に
同程度の幅で揺れて変化する

という条件を満たしていれば、定常性があると考えることができます。

トレンドが含まれているような「非定常」なデータは、差分をとったり、対数をとったりなどの加工して「定常」なデータとしてから時系列解析をします。

元のデータは非定常で、差分をとると定常となるデータを「単位根」といい、単位根があるかは「ADF検定」で調べることができます。やってみましょう。

# ADF検定
adf1=sm.tsa.stattools.adfuller(data['earnings'])
print(adf1)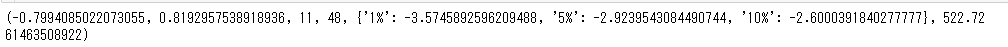

出力は左から順に、「検定統計量」「p値」「ラグの数」「データ数」「{棄却域}」「AIC値」となります。この検定では、

帰無仮説：「単位根（弱定常過程）が存在する」
対立仮説：「単位根は存在しない」

として検定をおこなっています。p値をみると帰無仮説は棄却されないので、単位根は存在しないとは言えない、ということになります。
※存在する、といえるわけではないので注意

定常性を持つデータに変換する

単位根は存在しないとは言えないので、データを「定常」なデータになるように加工していきましょう。まず、はじめに思いつくのが、差分をとる、という加工です。やってみましょう。

# 差分をとる
diff=data['earnings'].diff()
diff=diff.dropna()

# 差分をとったデータをADF検定する
adf2=sm.tsa.stattools.adfuller(diff)
print(adf2)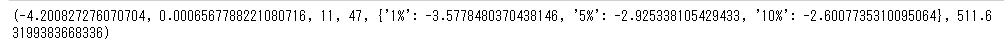

差分をとったデータを先ほどと同じようにADF検定しています。今度はp値が0.000656であるため、帰無仮説は棄却されます。

この差分をプロットしてみると、次のようになります。

# データの差分をプロット
fig,ax1=plt.subplots(figsize=(16,8))
ax2=plt.twinx(ax1)
ax1.plot(data['earnings'],color='orange',alpha=0.7,label='原系列')
ax2.plot(diff,label='差分系列')

ax1.set_ylim(0,1550)
ax2.set_ylim(-600,1550)


# 凡例
handler1, label1 = ax1.get_legend_handles_labels()
handler2, label2 = ax2.get_legend_handles_labels()
# 凡例をまとめて出力する
ax1.legend(handler1 + handler2, label1 + label2,fontsize=18)


plt.grid()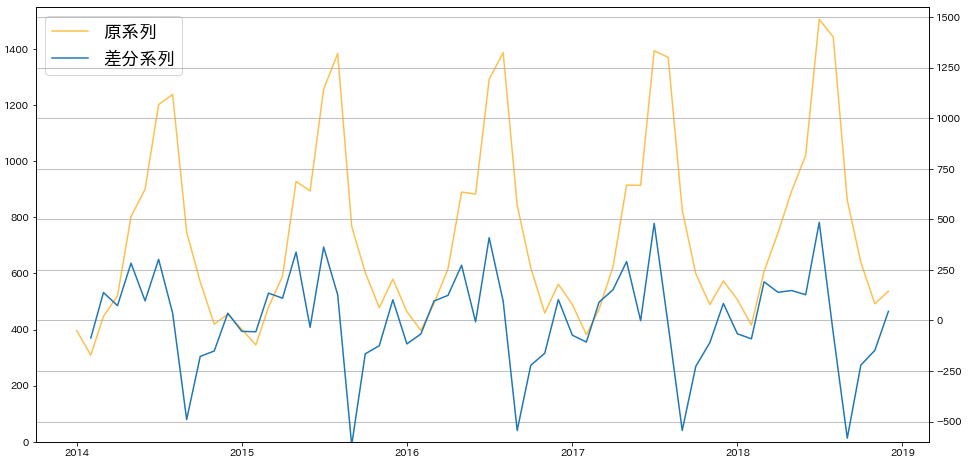

原系列には右肩上がりのトレンドがありましたが、差分系列は平均が一定っぽい感じになりました！

モデルの種類

ここまでで、非定常な時系列データを加工して定常なデータとすることができました。ここからは、モデルを作成して、予測にチャレンジしましょう。

まず、時系列分析の際の解析モデルについて、整理しておきましょう。

ARモデル（自己回帰モデル）：
AR(p)　※p時点過去までの値を使用する

$y_{t}=c+\Sigma_{i=1}^{p}\phi_{i}y_{t-1}+\epsilon_{t}$

$y_{t}$と$y_{t-1},y_{t-2},,,y_{t-p}$が相関を持つ。p期までのデータを使う場合には、AR(p)こと表現する。これは次のようにも表現できる。

$y=c+\phi y_{t-1}+\epsilon_{t}$

$\epsilon$は誤差項で、平均0、分散$\sigma^{2}$のホワイトノイズ
$|\phi|>1$となると発散して非定常となる
MAモデル（移動平均モデル）：
MA(ｑ）　※q時点過去までのノイズを使用する

$y_{t}=\mu+\Sigma_{i=1}^{q}\theta_{i}\epsilon_{t-i}+\epsilon_{t}$

q期までのデータの誤差の和を用いて表す。これをMA(q)と表現する。過去のノイズが大きかった場合は、現在の値も大きく変化する。
ARMAモデル（自己回帰移動平均モデル）：
ARMA(p,q)　※p時点過去のデータとq時点過去のノイズを使用する

$y_{t}=c+\Sigma_{i=1}^{p}\phi_{i}y_{t-i}+\epsilon_{t}+\Sigma_{j=1}^{q}\theta_{j}\epsilon_{t-j}$

p期前までのデータとq期前までの誤差の和を用いて現在のデータを表現するモデル。ARMA(p,q)と表現する。ARモデルとMAモデルから構成されるモデルと考えることもできる。
ARIMAモデル（自己回帰和分移動平均モデル）：
ARIMA(p,d,q)　※d階差分をとった系列に対してARMA( p,q) を考える

ARIMAモデルはAR、MAモデルに加えて差分系列の考えを組み合わせたもの。何度か差分をとると定常となるような非定常データを考えたモデル
SARIMAモデル（季節調整済みARIMAモデル）：
SARIMA(p,q,d)(P,D,Q)[s]
※時系列方向の説明にARIMA( p,d,qp,d,q ) モデルを使うだけでなく、周期方向の説明にもARIMA( P,D,QP,D,Q )モデルを使う

ARIMAモデルに、さらに周期的な変動（季節変動とか）を考えたモデル。ARIMAモデルとSARIMAモデルは、非定常過程のデータに対して適用できるのが大きな特徴です。