▶ この他にもいろんな前処理があります。対数変換に関する解説記事はこちらです。
はじめに
今回は外れ値の除外を扱います。外れ値とは、他の値から大きく外れた値のことです。外れ値の中でも外れ値となった理由があるものを異常値としています。外れ値を除外する場合は、通常、その外れ値が「異常値」である場合です。今回は四分位範囲を利用した方法、標準偏差を利用した方法を紹介します。
サンプルデータの作成
動物たちのテストの結果が与えられているとしましょう。100個の得点結果が与えられています。
# ライブラリのインポート
import pandas as pd
import numpy as np
pd.options.display.precision=1
# サンプルデータの作成
animals=['らくだ','らいおん','ねこ','ぞう','うし','うま','しまうま','うさぎ']
df=pd.DataFrame({'なまえ':random.choices(animals,k=100),
'得点':np.random.randint(55,86,100)})
df.head()
ここに外れ値として「らくだ」さんが100点をとったレコードと、「ねこ」さんが23点をとったレコードを加えておきましょう。
# 外れ値を加える
df.loc[100]=['らくだ',100]
df.loc[101]=['ねこ',23]
df.tail()
外れ値の除外
このデータのうち、得点の外れ値を抽出してみましょう。ここでは、四分位数を用いる方法と、標準偏差を用いる方法をご紹介しましょう。
四分位範囲を利用した外れ値の除外
外れ値をどのように定義するかはその時にもよりますが、ここでは四分位範囲を用いた方法を紹介します。第三四分位数から第一四分位数を引いたものをIQRと表記し、これを四分位範囲といいます。
このIQRに1.5をかけて第一四分位数から引いたものを下限、IQRに1.5をかけて第三四分位数に加えたものを上限として、この範囲から外れたものを「外れ値」とします。やってみましょう。
# 四分位数、四分位範囲
q1=df['得点'].quantile(.25)
q3=df['得点'].quantile(.75)
iqr=q3-q1
print('第一四分位数は%.1fです'%q1)
print('第三四分位数は%.1fです'%q3)
print('四分位範囲は%.1fです'%iqr)
limit_low=q1-iqr*1.5
limit_high=q3+iqr*1.5
print('下限は%.1fです'%limit_low)
print('上限は%.1f'%limit_high)
ここまで算出できれば、あとは簡単ですね。query()メソッドで簡単に抽出することができます。
df.query('not @limit_low < 得点 < @limit_high')
一応、分布をみておきましょう。
plt.boxplot(df['得点'])
plt.title('得点の分布(箱ひげ図)')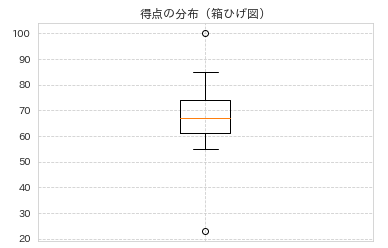
標準偏差を用いた外れ値の除外
次に標準偏差を用いる方法も紹介しておきます。こちらも、外れ値を決める必要がありますが、ここでは「平均±3σ」の範囲を外れるもの、としましょう。
# 平均と標準偏差を算出
point_mean=df['得点'].mean()
point_sigma=df['得点'].std()
# 下限と上限を算出
limit_low2=point_mean-3*sigma
limit_high2=point_mean+3*sigma
print('得点の平均は%.1fです'%point_mean)
print('得点の標準偏差は%.1fです'%point_sigma)
print('下限は%.1fです'%limit_low2)
print('上限は%.1fです'%limit_high2)
ここまでくれば、同じようにquery()メソッドで外れ値を抽出できますね。
df.query('not @limit_low2 < 得点 < @limit_high2')
まとめ
いかがでしょうか?外れ値を除去する場合、理由がわかっている「異常値」であることと、定量的な定義が必要になります。よく抑えておきましょう。
▶ 一気にデータの概要を把握する方法があります。こちらの記事をどうぞ。




コメント