- 時系列データの処理の仕方を知らない、または、基本から学びたい方
- 時系列データを扱ったことがあるが、体系的に整理できていないので学びなおしたい方
はじめに
今回は時系列データの取り扱いを基本から解説していきましょう。テーブルデータ的な取り扱いをすることもありますが、時系列データ特有の処理の仕方があります。まずは、時系列データの特徴の整理からはじめて、実際の処理の仕方を基本から解説していきます。
時系列データについて
時系列データ解析とは、時間の経過ともに観測されたデータを、統計的に解析することで変化の規則性を見出したり、予測に役立つ情報を得る解析手法のことです。まずは、時系列データの特徴からみていきましょう。
時系列データの特徴
時系列データでは、データの前後に関係があります。(自己相関といいます)また、季節性・周期性があるのも大きな特徴となります。周期性とは別にトレンド(非定常過程)があります。その他、外因の影響を受けたり、ホワイトノイズを含むといった特徴があります。
時系列データ分析の目的
時系列データ分析の目的は、おおきくわけて次の二つがあります。
- 過去データに対する解釈
- 未知データに対する予測
過去データに対する解釈は、「周期性の把握」「トレンドの把握」です。一方、未知データに対する予測では、ビジネス課題に対して何が予測できれば解決するのかをよく考える必要があります。たとえば、「予測したい粒度はどのくらいか?(商品カテゴリ別なのか?商品ごとなのか?)」「予測したい時期・期間はどのくらいか?(1週間後を予測したいのか?1か月後を予測したいのか?)」のようなことを検討する必要があります。
定常過程と非定常過程
時間によらず期待値、自己共分散が一定である時系列データの性質を定常性といいます。
観測されたデータの平均と分散が一致するので、一定の値で振動するような図となる。定常性をもったデータは分析しやすいが、一方で、現実に扱うほとんどの時系列データは非定常性となる。非定常データでは、期待値が時点によって変化する、つまりトレンドがある。
非定常データでも、データの差分やlogなどデータの変換をすると定常性を持つことが多く、このような変換を用いて時系列データの解析を進めることになる。
ホワイトノイズ
データ範囲が一定の範囲に収まる、という特徴があります。定常過程です。全ての周波数帯域においてエネルギーが均一に混入した雑音のこと。「ホワイト」とは、可視領域の広い範囲をまんべんなく含んだ光が白色であることから来ている形容だそうです。(Wikipedia)
次はまず、このホワイトノイズを実装してみましょう。
実装
まずは必要なライブラリのインポートをしておきましょう。
# ライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inlineホワイトノイズ
まずばサンプルデータを作成しましょう。
# サンプル数の指定
n_sample=1000
# ホワイトノイズのarrayを作成
np.random.seed(0)
x_wn = np.random.randn(n_sample)
np.random.seed(42)
y_wn = np.random.randn(n_sample)
# data frameに格納
df_random = pd.DataFrame({'x_wn':x_wn, 'y_wn':y_wn})
df_random.head()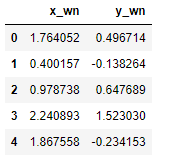
numpyのrandomモジュールのrandnは、平均0、分散1(標準偏差1)の正規分布の乱数を発生させます。引数に指定した数だけ発生させます。ここでは、2つの異なるホワイトノイズ、x_wnとy_wnを作っています。それぞれ再現性を持たせるためにseedを固定しています。これを扱いやすいようにデータフレームに格納しています。
これをプロットしておきましょう。
# ホワイトノイズを時系列順にプロットする
plt.figure(figsize=(12,6))
plt.plot(df_random.index, df_random['x_wn'], label='x_wn')
plt.plot(df_random.index, df_random['y_wn'], label='y_wn')
plt.legend(fontsize=15)
plt.title('ホワイトノイズ',fontsize=18)
plt.grid()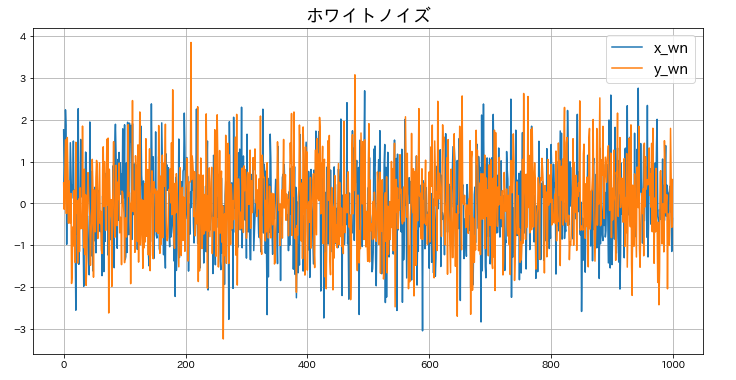
データは一定の幅に収まっているといえるでしょう。2つのホワイトノイズ、x_wn、y_wnの相関もみておきましょう。次は散布図をプロットします。
# ホワイトノイズxとホワイトノイズyの関係
plt.figure(figsize=(8,8))
plt.scatter(df_random['x_wn'], df_random['y_wn'])
plt.xlabel('x_wn',fontsize=15)
plt.ylabel('y_wn',fontsize=15)
plt.title('ホワイトノイズ',fontsize=18)
plt.grid()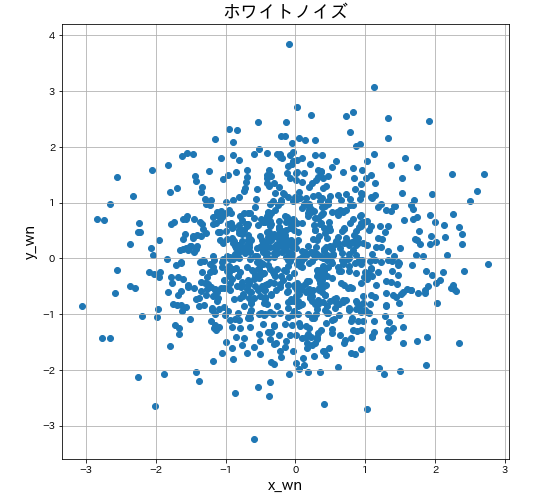
この例のデータでは、全く相関はみられないですね。
既にmatplotlibには慣れてますか?可視化に苦手意識がある方は、何回かにわたって可視化の基本を解説した記事があるので、この記事から読み進めてください。
ランダムウォーク
次にランダムウォークです。ランダムウォークとは、次に現れる位置が確率的に無作為(ランダム)に決定される運動のことです。こちらもまずサンプルデータを作成しましょう。
# ホワイトノイズの累積和はランダムウォークになる
df_random['x_rw'] = df_random['x_wn'].cumsum()
df_random['y_rw'] = df_random['y_wn'].cumsum()
df_random.head()次に現れる位置が確率的に無作為(ランダム)なので、累積和を列を作ればそれがrandomウォークそのものになりますね。ここではx_rwとy_rwを作りました。
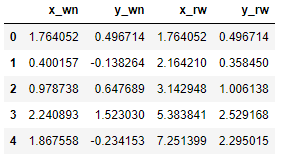
次に可視化を行います。先ほどの同様の要領でプロットします。
# ランダムウォーク
plt.figure(figsize=(12,6))
plt.plot(df_random.index, df_random['x_rw'], label='x_rw')
plt.plot(df_random.index, df_random['y_rw'], label='y_rw')
plt.legend(fontsize=15)
plt.title('ランダムウォーク',fontsize=18)
plt.grid()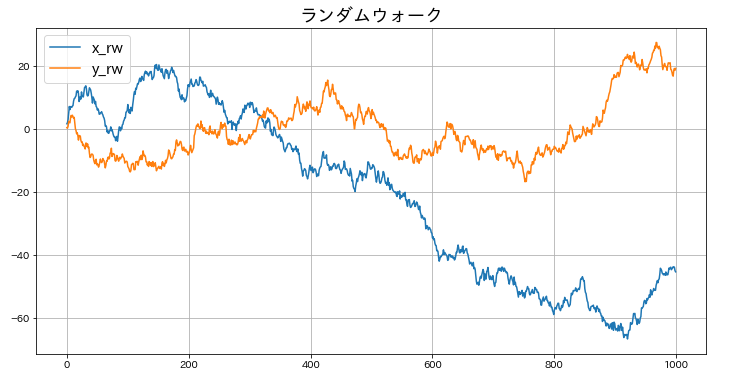
次に相関をみてみましょう。
plt.figure(figsize=(8,8))
plt.scatter(df_random['x_rw'], df_random['y_rw'])
plt.xlabel('x_rw',fontsize=15)
plt.ylabel('y_rw',fontsize=15)
plt.title('ランダムウォーク',fontsize=18)
plt.grid()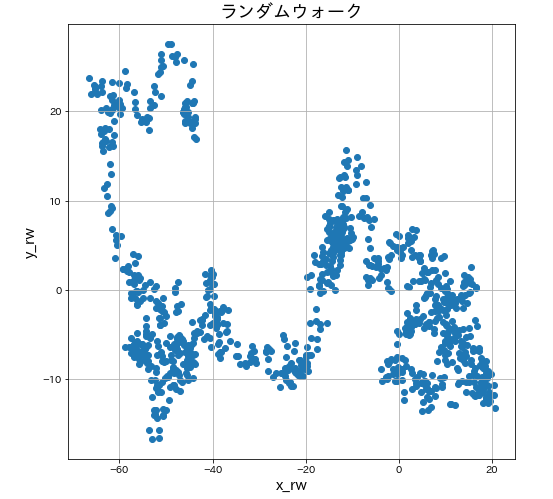
線形な関係はなさそうですね。
まとめ
いかがでしたか?今回は時系列データの基礎として、ホワイトノイズ、ランダムウォークを扱いました。まずはこの辺の基礎を固めておくことが、このあとの時系列データ解析をするうえで重要となりますので、しっかりおさえておきましょう。次は、時系列データの予測モデル作成に進みましょう。
▶データ分析を基本から学びたい場合は、以下の記事も参考にしてください。




コメント