- データを分析をしたいが、どこから始めてよいかわからない方
- データを仕事に活かしたいが、データの解釈の仕方がわからない方
- 統計学を体系的に学んだことがない、初学者の方
▶ 統計学の初学者向けに記事を書いています。はじめから読む場合は以下をどうぞ
はじめに
統計学を学んだことがない初学者を対象にして、基本から解説しています。今回はPythonで「正規性の検定」する方法を基本から解説していきます。検定自体は1行のコードで済みますが、Q-Qプロットなどで視覚的に確認することも重要です。今回はQ-Qプロットとその描き方を解説して、その次に「シャピロ-ウィルクの検定」で正規性を検定する方法を扱います。
Q-Qプロット
Q-Qプロットは、Quantile-Quantileプロットの略です。Quantileは分位数でしたね。Q-Qプロットは、得られたデータが理論上の分布にどのくらい近いかを視覚的に確認することができます。データが理論上の分布を表した直線状付近にプロットされていれば、その分布から得られたデータと考えることができます。逆に、直線から離れているデータがあると、その分布から得られたデータではないと考えます。
シャピロ-ウィルクの検定
準備
正規性の検定にはいくつかあり、そのひとつにシャピロ-ウィルクの検定があります。Pythonでシャピロ-ウィルクの検定をおこなうには、scipyライブラリのstatsモジュールにあるshapiro()を使います。はじめにこのshapiro()の使い方を整理しておきましょう。
xには正規性がどうかを検定するデータをいれます。戻り値はt検定のときのように第一の戻り値は検定統計量、第二の戻り値はp値となります。これらは忘れてしまっても、「Shift + Tab」でDocstringで確認することができます。

次にQ-Qプロットの実装方法も確認しておきましょう。Q-Qプロットは、statsmodelsというライブラリを用います。この中にあるapi.qqplot()メソッドを使います。これも整理しておきましょう。
先にDocstringを確認しておきましょう。
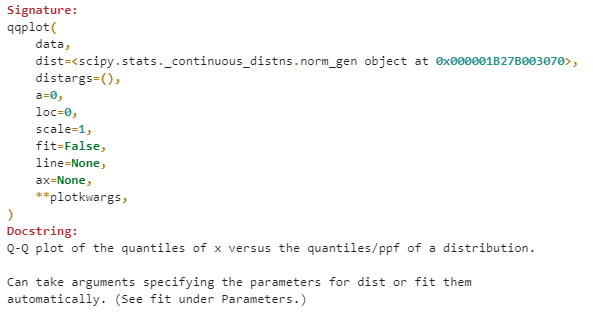


dataには正規性を確認するデータをいれます。lineパラメータにはr(regression:回帰)を指定します。このqqplot()メソッドでは、関数内で描画がされます。さらにReturnsをみるとFigureが返ってくるため、2つ描画されてしまいます。2つ描画されることを避けたければ、変数として受けておけばよいでしょう。
問題の設定
前回、正規性の検定をせずにスチューデントのt検定とウェルチのt検定を扱いました。いずれの場合も正規性が仮定されるため、本来であれば正規性の検定が必要です。今回は、前回と同じデータセットで正規性の検定をすることにしましょう。
▶ スチューデントのt検定、ウェルチのt検定については以下の投稿をどうぞ。
早速データセットを用意しましょう。
# ライブラリのインポート
import pandas as pd
import numpy as np
from scipy import stats
from statsmodels.api import qqplot
import seaborn as sns
# データセットのロード
df_taxis=sns.load_dataset('taxis')
# 2群の作成
df_credit=df_taxis.query('payment=="credit card"')['fare']
df_cash=df_taxis.query('payment=="cash"')['fare']
# データの確認
print(df_credit.head())
print(df_cash.head())支払方法がクレジットカードの場合の運賃のデータである「df_credit」と支払方法がcashの場合の運賃のデータである「df_cash」という標本があります。これらの母集団に正規性があるかどうかを検定することにしましょう。
帰無仮説と対立仮説
検定の手順にだいぶ慣れてきましたね。まず帰無仮説と対立仮説をたてるのでしたね。ただ「正規性の検定」ではこれまでとちょっと違うところがあるので注意が必要です。これまでは、棄却されることを期待した仮説を帰無仮説に設定して、成立させたい仮説を対立仮説に設定していました。
「正規性の検定」では、帰無仮説は「母集団が正規分布に従う」を設定し、対立仮説は「母集団が正規分布に従わない」となります。
これまでは、帰無仮説は棄却することを期待して棄却できれば対立仮説を成立させる、棄却できなかった場合には、帰無仮説を棄却できなかった、というにとどめて、積極的に帰無仮説を採択することはありませんでした。
それに対して、「正規性の検定」では帰無仮説が成立することを期待しています。ただ、帰無仮説を棄却できなかった場合に、必ず帰無仮説が成立することを言えるわけではない点はこれまでと同じです。そのため、「正規性があることを棄却できなかった」ということになります。
※ややこしいですが、正規性がある、とまでは言い切れず、正規性があることを否定できない、ということになります。
Pythonによる正規性の検定
早速、シャピロウィルクの検定をやってみましょう。まずはdf_creditからです。
# シャピロ-ウィルクの検定(df_credit)
stats.shapiro(df_credit)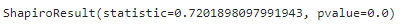
p値が0になってしまいました。有意水準5%以下なので当然棄却域に入ります。今回は、df_creditの母集団は正規性はない、ということになります。
続いて、df_cashについても見ておきましょう。
# シャピロ-ウィルクの検定(df_cash)
stats.shapiro(df_cash)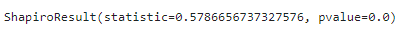
こちらも同様に棄却域に入るため、母集団には正規性はない、という結果になります。どちらも正規性がない、という結果になってしまいましたが、これを視覚的に確認しておきましょう。
Q-Qプロットで視覚的に確認
まずはdf_creditからみておきましょう。
# Q-Qプロット(df_credit)
fig=qqplot(df_credit,line='r')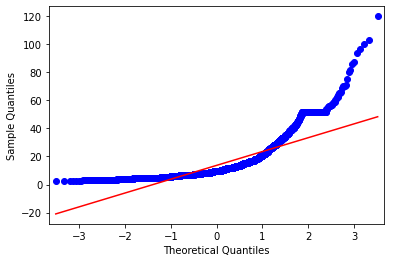
Q-Qプロットを見てみると、データ(青い点)は理論上の分布(赤い線)上から大きく離れてしまっており、確かに正規性がなさそうですね。ヒストグラムも見ておきましょう。
# ヒストグラム(df_credit)
sns.displot(df_credit)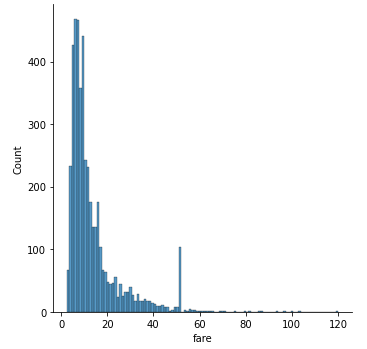
40~60の間に急にスパイクしている部分がありますね。正規分布とは言えなそうです。同様にdf_cashもみてみましょう。まずはQ-Qプロットからです。
# Q-Qプロット(df_cash)
fig=qqplot(df_cash,line='r')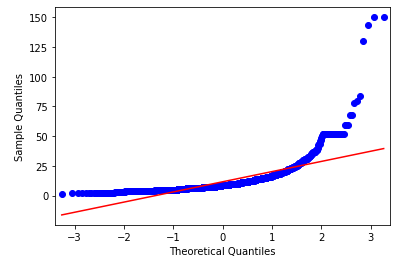
こちらも理論上の直線から大きくかけ離れているため、正規分布とはいえなそうですね。ヒストグラムも確認しておきましょう。
# ヒストグラム(df_cash)
sns.displot(df_cash)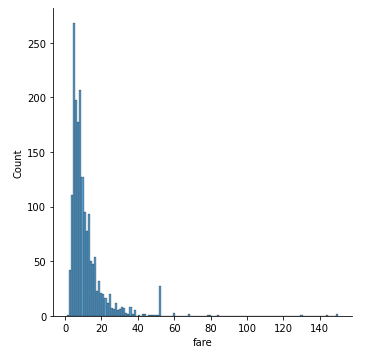
こちらも40-60にスパイクがあり、正規分布になっていなそうですね。
まとめ
正規性の検定をする方法はいくつかありますが、今回はその中でもシャピロ-ウィルクの検定を扱いました。視覚的に確認する方法としてQ-Qプロットを合わせて利用したり、ヒストグラムを描いて確認するのもよい方法です。これらもあわせて解説しました。ただ、検定して終わり、ではなくプロットを描いて確認する癖をつけておくとよいですね。




コメント