Python初心者向け：分散/標準偏差を基本から解説します

▶ まずデータの概要をつかむなら、以下の記事を参考にしてください。基本統計量をまとめて算出する方法をご紹介しています。

Python初心者でも簡単にデータの概要を把握できるように基本から解説します。分析を始める前にデータの概要を把握することが大切です。やみくもにデータと向き合うのではなく、どのような特徴があるのか概要をつかむことで、データ分析の方針をたてることができます。

はじめに

今回は分散と標準偏差を扱います。分散には標本分散と不偏分散、標準偏差には標本標準偏差と不偏標準偏差とがあります。ややこしいのは、使うライブラリによってdefaultで計算するものが異なる点です。pandasとnumpyでdefaultで異なるので、特にこの辺を意識して整理しておきましょう。

標本分散と不偏分散

分散は、「データが平均値からどれだけ離れているか」をあらわします。定義は次の式となります。

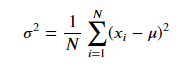
この分散は、正確には標本分散と呼ばれます。標本分散は母集団の分散（母分散）と比べて分散を過小評価してしまう、というバイアスがあります。これを修正したものが不偏分散となります。その定義式は次のようになります。

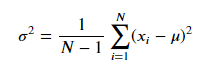
不偏分散は、標本分散の期待値が母分散に一致するように標本分散の算出式にN/(N-1)をかけたものです。したがって、不偏分散は一致性と不偏性をもつ推定量となります。

標本標準偏差と不偏標準偏差

標準偏差は、分散の平方根をとったものです。分散に標本分散と不偏分散があるように、標準偏差にも標本標準偏差と不偏標準偏差があります。

numpyとpandas<

numpyにもpandasにも分散や標準偏差を計算するメソッドが用意されています。分散は、numpyでもpandasでもvar()メソッドで求めることができますが、それぞれがdefaultで計算するものが異なるので注意が必要です。

それではさっそくみていきましょう。

# ライブラリのインポート
import pandas as pd
import numpy as np

# テストデータ
test_data_numpy=np.array([1,3,5,7,9])
test_data_pandas=pd.Series([1,3,5,7,9])

このデータの分散を求めてみましょう。まずは、var()メソッドを使わずに計算してみましょう。

mean=test_data_pandas.mean()

std_manual=0
for i in test_data_pandas:
    std_manual+=(mean-i)**2

print('標本分散の値は%.1f'%(std_manual/(5))) 
print('不偏分散の値は%.1f'%(std_manual/(5-1)))

このように標本分散と不偏分散を求めることができました。次に、numpyとpandasのvar（）メソッドで求めてみましょう。

print('numpyは%.1f'%test_data_numpy.var())
print('pandasは%.1f'%test_data_pandas.var())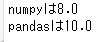

つまり、numpyでは標本分散、pandasでは不偏分散となります。numpyで不偏分散を求めたいときには、ddof=1を指定することで求めることができます。

print('numpyで不偏分散を求めると%.1f'%test_data_numpy.var(ddof=1))

同じようにpandasで標本分散を求めるときには、ddof=0を指定することで算出できます。

print('npandasで標本分散を求めとは%.1f'%test_data_pandas.var(ddof=0))

標準偏差でも同じことが起こります。

print('numpyは%.1f'%test_data_numpy.std())
print('pandasは%.1f'%test_data_pandas.std())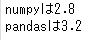

numpyでddof=1を指定すれば、pandasと同じ値となります。確認しておきましょう。

print('numpyで不偏標準偏差を求めると%.1f'%test_data_numpy.std(ddof=1))

まとめ

いかがでしょうか？この辺はややこしいですね。メソッド名が同じvar()やstd()なのにその中身の計算が異なります。よく整理しておきましょう。

▶ 最頻値に関する記事をあります。こちらから参照してください。

Python初心者向け：最頻値を基本から解説

Python初心者向けに最頻値を基本から解説します。最頻値は『一番出現頻度の高い値』のことです。シリーズを対象とする場合、データフレームを対象とする場合を例に解説します。最後にgある特徴量ごとに別の特徴量の最頻値を求める例を見ていきましょう。

▶ 四分位数やこれを使った外れ値の除外に関する記事もあります。

Python初心者向け：四分位数/標準偏差を用いた外れ値の除外

Python初心者向けに四分位数や標準偏差を用いて外れ値を除外する方法を基本から解説します。外れ値とは他の値から大きく外れた値です。外れ値の中でも外れ値となった理由があるものを異常値といいます。外れ値を除外するは、通常、「異常値」を除外します。

▶ 一気にデータの概要を把握する方法があります。こちらの記事をどうぞ。

Python初心者向け：分散/標準偏差を基本から解説します