統計学：初学者向けに標準化を基本から解説します

この記事はこんな方におススメです

データを分析をしたいが、どこから始めてよいかわからない方
データを仕事に活かしたいが、データの解釈の仕方がわからない方
統計学を体系的に学んだことがない、初学者の方

▶ まず正規分布について学びたい方は以下の記事もご覧ください。

今回は統計学ではおなじみの正規分布を確認していきましょう。正規分布はガウスが発見したので、ガウス分布とも呼ばれます。この正規分布は自然界でも多く見られ、統計学の分野でもよく使われる分布です。まずは定義から確認してPythonで確かめていくことにしましょう。

はじめに

統計学を学んだことがない初学者の方を対象にして基礎から解説しています。今回は「標準化」を扱います。データを集めたあと「比較」をすることでその値が大きいのか小さいのかを判断することができます。しかし、「尺度」が揃っていないと比較をすることもできません。「標準化」をすることによって尺度を揃え比較できるようになります。標準化の定義を確認し、Pythonでの実装方法まで確認していきましょう。

標準化（T-score）

異なる尺度のデータを比較できるように、あるデータがすべてのデータの分布の中でどこに位置しているのか、を考えます。すべてのデータの分布を「標準化」によって揃えておけば、比較することができますね。

英語が98点、数学が90点だとしても、必ずしも英語のほうがよい、とはいえません。それはほかの生徒の英語の得点にもよるからです。英語の平均点が95点の時に98点取ったのと、数学の平均点が70点の時に90点とったのをそのままは比較できない、ですよね。

この標準化は、「平均を0、分散を1にすること（ｚ得点という）」です。各データをx, データの平均値を$\bar{x}$、標準偏差を$s$とすると、数式では以下のように表現できます。
※標本の標準偏差はs、母集団の標準偏差は$\sigma$であらわすことが多い

\[ z=\frac{x-\bar{x}}{s} \]

偏差値（Z-score）

偏差値はこれまでの中学・高校の教育の中でも耳にすることが多かったと思います。この偏差値は「標準化」を応用したものと言えます。標準化は平均を0、標準偏差を1でしたが、偏差値は平均を50、標準偏差を10にしたものです。（T得点といいます）

このように偏差値を用いると、（平均が50、標準偏差が10なので）次のようになります。

40～60の区間に全データの約68%が収まる
30～70の区間に全データの約95%が収まる
20～80の区間に全データの約99.7%が収まる

先ほどの英語や数学の点数だけが与えられた状態では比較できませんでしたが、「偏差値」にしておくと、上記の特性から全データのどの位置なのかが想像できますね。

Pythonで標準化する

各データから平均を引いて標準偏差で割る処理なので、直接計算することもできますが、ここではscikit-learnというライブラリのpreprocessingというモジュールを使って標準化してみましょう。

▶ 直接計算するやり方は、以下の投稿で扱っていますので、参考にしてください。

Python初心者向け：標準化/正規化という用語の使い分けについて

Python初心者向けにデータの前処理である準化・正規化について基本から解説します。この用語の明確な使い分けが定義されているわけではないようです。ここでは、各項目を説明する前に、このブログの中での意味の使い分けを説明しておきます。

preprocessingの中には、StandardScaler()というクラスがあります。これを利用して標準化をしてみましょう。次の手順で標準化することができます。

StandardScaler()でインスタンスを作る
作成したインスタンスに対してfit_transform(data)とする

早速、やってみることにしましょう。

# ライブラリのインポート
import numpy as np
import seaborn as sns
from sklearn.preprocessing import StandardScaler

# データの読み込み
df_taxis=sns.load_dataset('taxis')
df_taxis.head()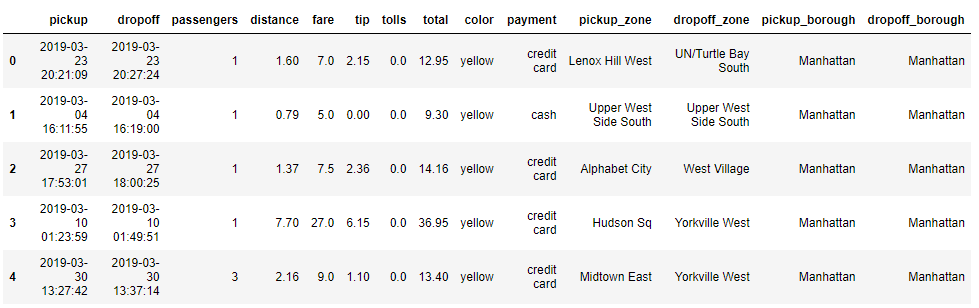

今回はseabornライブラリに用意されているtaxisというデータセットを使うことにしましょう。このデータの「fare」を標準化します。

▶ seabornライブラリに用意されているデータセットの扱い方は以下をどうぞ。

Python初心者向け：seabornの学習用データセットの使い方を基本から解説

データ分析の学習を進めていると、実際にデータを使って試してみたくなることがあるでしょう。サンプルデータを一から作るのは大変です。ぜひ、学習用に用意されたデータセットを使ってみてください。この記事を読むと、Seabornの学習用データセットを扱うことができるようになります。

まずはStandardScaler()でインスタンスを作ります。そのあと、このインスタンスに対して、fit_transform(data)とするのでした。この際に、「data」の部分は二次元のデータである必要があります。そのため、ある一つの特徴量のみを変換するときには注意が必要です。次のように一度、.valuesでnp.arrayに変換し、さらにreshape(-1,1)で二次元データに変換します。

やってみましょう。

# インスタンスの作成
scaler=StandardScaler()

# 標準化
scaled=scaler.fit_transform(df_taxis['fare'].values.reshape(-1,1))
print(scaled)

これを偏差値にするには10を掛けて50を加えればよかったですね。

# 偏差値を算出
t_score=scaled*10+50
print(t_score)

簡単ですね。特徴量が１つの場合には、.values（numpyのarrayに変換）→reshape（2次元データに変換）としましたが、特徴量が2つ以上ある場合はデータフレームを直接指定すればOKです。こちらも確認しておきましょう。

# インスタンスを作成
scaler2=StandardScaler()

# 標準化
scaled2=scaler2.fit_transform(df_taxis[['fare','tip']])
print(scaled2)

fareとtipを標準化しました。1列目のデータは先ほどのデータと一致してますね。

まとめ

今回は標準化を扱いました。また標準化の応用として偏差値の考え方と、Pythonでの実装方法を扱いました。標準化は定義に沿って、みずから実装しても難しくありませんが、scikit-learnのprocessingモジュールにあるStandardScaler()というクラスを使うと簡単に計算することができます。scikit-learnは機械学習用のライブラリなので、ベースとして二次元のデータを扱うように設計されていることに注意してください。