統計学：初学者向けにPythonで正規分布を扱う方法を基本から解説

はじめに

統計学を学んだことがない初学者を対象にして基礎から解説しています。今回は統計学ではおなじみの正規分布を確認していきましょう。正規分布はガウスが発見したので、ガウス分布とも呼ばれます。この正規分布は自然界でも多く見られ、統計学の分野でもよく使われる分布です。まずは定義から確認してPythonで確かめていくことにしましょう。

正規分布

既に何度か扱っている正規分布ですが、あらためて定義を確認しておきましょう。平均を$\mu$分散を$\sigma^{2}$とする正規分布の確率密度関数は以下で与えられます。

\[ \displaystyle f(x) = \frac{1}{\sqrt{2\pi \sigma^{2}}} \exp \left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \]

Pythonで正規分布を扱う際には、この数式を覚えている必要はなく、scipyライブラリのstatsモジュールにあるnorm()を利用するだけですみます。見ていきましょう。

# ライブラリのインポート
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
%matplotlib inline

# 正規分布の描画
x=np.linspace(-5,5)
y=stats.norm(loc=0,scale=1).pdf(x)

plt.plot(x,y)
plt.grid()
plt.title('平均0, 標準偏差1の正規分布')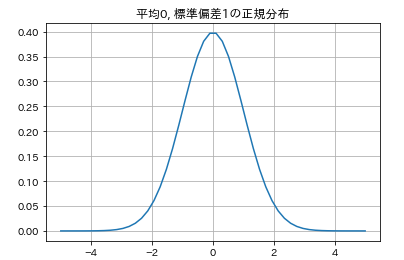

norm()の中ではlocで平均値($\mu$)、scale($\sigma$)で標準偏差を指定しています。正規分布は平均値$\mu$と(標準偏差を2乗した)分散$\sigma^2$で決まるため、N($\mu,\sigma^2$)と表現することがあります。また、確率変数Xが正規分布N($\mu,\sigma^2$)に従うとき、次のように表現します。

\[ X \sim N(\mu,\sigma^2)\]

norm()ではloc,scaleで平均値、標準偏差を指定することができますが、これらの指定を省略すると、平均値0、標準偏差1の正規分布が得られます。このような平均値0, 標準偏差1の正規分布を標準正規分布といいます。

ところで、平均値$\mu$と標準偏差$\sigma$がわかると次のことがわかります。

カーネル密度推定（KDE：Kernel Density Estimation）

カーネル密度推定は、手元にあるデータ（観測した分布）から確率密度関数（確率分布）を推定する手法です。連続型の分布について使うものです。カーネル密度推定はたとえば、手元にあるデータから同じような分布をもうひとつ作りたいときに、一度カーネル密度推定をしてそこからランダムにデータを取り出す、というような操作をします。

実際にPythonで確認していきましょう。これまで同じようにscipyライブラリのstatsモジュールを使います。statsモジュールにgaussian_kde()というメソッドが用意されています。

手元にあるデータが推定をするので、引数には「データ」を指定します。また、このgaussian_kde()にはあらたなデータを取得するresample()というメソッドやpdf()が用意されています。やってみましょう。

# データ
data=[1,3,4,7,9,2,3,5,4,2,6,8,2]

# カーネル密度推定
x=np.linspace(-15,15)
y=stats.gaussian_kde(data).pdf(x)

# 描画
plt.plot(x,y)
plt.title('カーネル密度推定')
plt.grid()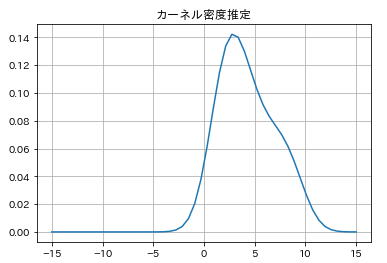

データから推定された確率密度関数を描画することができました。カーネル密度推定は、seabornを使って、ヒストグラムと合わせて描画することもできます。

# seabornでヒストグラムとカーネル密度推定の描画
sns.displot(data,kde=True,height=4,aspect=1.3)
plt.title('ヒストグラムとカーネル密度関数')
plt.grid()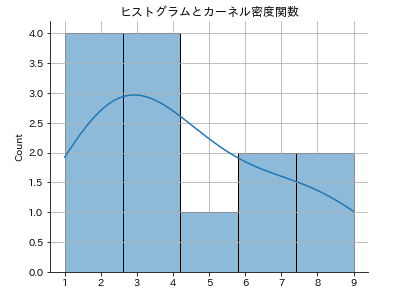

先ほどとだいぶ形状が違うように見えますが、これはヒストグラムと合わせて描いているからです。kdeだけを描いてみましょう。

# seabornでカーネル密度推定の描画
sns.displot(data,kind='kde',height=4,aspect=1.3)
plt.title('カーネル密度関数')
plt.grid()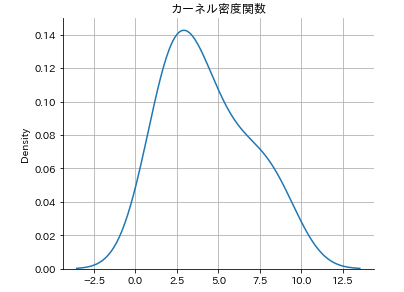

横軸の範囲が異なりますが、先ほどのstatsモジュールで描いた場合と同じ形状になっていることがわかるかと思います。

推定した分布からデータを抽出する

次に推定した分布からデータを抽出してみましょう。resample()というメソッドが用意されてましたね。

y2=stats.gaussian_kde(resamples).pdf(x)
plt.plot(x,y,label='original')
plt.plot(x,y2,label='resample')
plt.grid()
plt.legend(fontsize=15)
plt.title('カーネル密度推定の描画')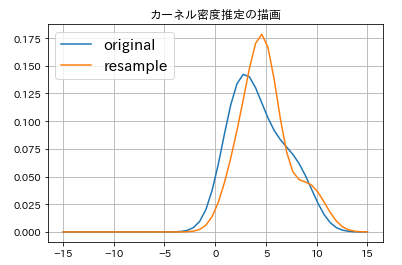

いかがでしょうか？推定値がresampleしたデータから、再度カーネル密度推定をしたものが、似たような形状となっていますね。

最後に推定した分布からデータを抽出する際の注意点を説明しておきます。カーネル密度推定はデータから確率密度関数を推定するので、resampleした際に実際には取り得ない値が抽出されることがあります。たとえば、0より小さい値をとることがないような場合に、再抽出したデータにはマイナスの値が含まれる、などのようなケースです。このような場合はいろいろな処理がありますが、境界でミラーリングする、という方法がとられることがあります。これも見ておきましょう。

たとえば、工場で生成するある部品の質量を測定したデータ(data2)があったとしましょう。部品の質量ですから、負の値はありません。これをカーネル密度推定してみましょう。

# データ
data2=[0.01,0.05,0.03,0.15,0.01,0.01,0.02,0.01,0.01]

# カーネル密度推定の描画
gaussian_kde2=stats.gaussian_kde(data2)
x2=np.linspace(-5,5)
y2=gaussian_kde2.pdf(x2)

plt.plot(x,y)
plt.grid()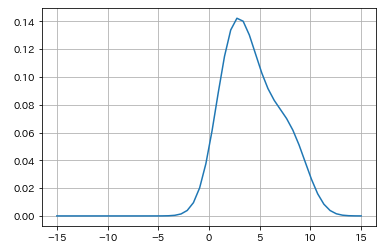

すると、このようにマイナスの領域にもプロットされてしまいます。そのため、この推定した分布からデータを生成すると、負の値が出てくる可能性があります。実際に見てみましょう。

# 推定した分布からデータを生成する
resamples2=gaussian_kde2.resample()
print(resamples2)

このように負の値も含まれていますね。そこで、負の値をとらないのであれば、０を境界線と考えてミラーリングするという処理をすることがあります。0を境界とした場合であると次のようにできます。

# 生成するデータを入れる空のリストを作成
resample_data=[]

# 正のものはそのまま、負のものはマイナスを乗じて追加
for data in resamples2[0]:
    if data>0:
        resample_data.append(data)
    else:
        resample_data.append(-data)

print(resample_data)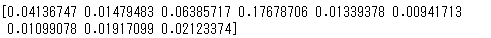

今回は0が境界となるため、負の場合はマイナスを乗じています。一般化すると、「2×（境界）-　data」となります。

まとめ

今回は正規分布を扱いました。schipyライブラリのstatsモジュールに用意されているstats.norm()で簡単に正規分布を扱うことができます。正規分布は、平均と標準偏差（$\sigma$）の２つのパラメータで形状が決まります。stats.norm()では、locで平均、scaleで標準偏差を指定することができます。

観測データから確率密度関数を推定する方法としてカーネル密度推定がある。カーネル密度推定をすることで、分布の比較などもしやすくなる。また、あらたに同じような分布からデータを取り出したい場合にも利用されます。