- データを分析をしたいが、どこから始めてよいかわからない方
- データを仕事に活かしたいが、データの解釈の仕方がわからない方
- 統計学を体系的に学んだことがない、初学者の方
はじめに
統計学を学んだことがない初学者の方を対象にして基礎から解説しています。今回は確率分布の一つとである「二項分布」を扱います。確率分布としては、既に一様分布や正規分布を扱っていますね。この二項分布はいろいろな確率分布の基礎となる分布であり、正規分布をこの二項分布から派生したものです。二項分布はどんなものであるかの解説からはじめて、Pythonでの実装までみていきましょう。
二項分布(Binomial distribution)
二項分布
二項分布を説明する前に、これまで扱った一様分布や正規分布を復習しておきましょう。
▶ 正規分布の定義やPythonでの実装はこちらの記事をどうぞ
では、二項分布はどのようば分布でしょうか?wikipediaを調べてみると、
二項分布(にこうぶんぷ、英: binomial distribution)は、結果が成功か失敗のいずれかである試行(ベルヌーイ試行と呼ばれる)を独立に n 回行ったときの成功回数を確率変数とする離散確率分布である。
https://ja.wikipedia.org/wiki/%E4%BA%8C%E9%A0%85%E5%88%86%E5%B8%83
とあります。わかりますか?
結果が成功か失敗の2つしかない試行を複数回おこなったときの成功(あるいは失敗)回数とはどのような確率変数かわかりますか?
たとえば、「サイコロを振って1がでるかでないか」という試行は成功か失敗しかないですね。これを複数回おこなったときの「1の目が出る回数」という確率変数が考えられます。サイコロを振って1が出る確率は1/6なので、たとえば3回試行をおこなって1の目が1回出る確率は、
- 1回目に1が出て残りの2回は1以外の目が出る(1/6×5/6×5/6=25/216)
- 2回目に1が出て1回目と3回目は1以外の目が出る(5/6×1/6×5/6=25/216)
- 3回目に1が出て1回目と2回目は1以外の目が出る(5/6×5/6×1/6=25/216)
となるので、25/216 + 25/216 + 25/216 = 75/216 = 25/72と計算できます。これを一般化すると次のように表現できます。
先ほどのサイコロを3回振って1の目が1回出る確率は、p=1/6, n=3, k=1ですね。これを当てはめてみると、
\[_3C_1\left( \frac{1}{6} \right)^1\left( \frac{5}{6} \right)^{3-1}=3 \times \frac{1}{6} \times \frac{25}{36} = \frac{25}{72} \]
となり、先の結果と一致しますね。
Pythonによる実装
Pythonで二項分布を扱う場合もscipyライブラリのstatsモジュールを使います。二項分布の確率分布はbinom(n, p)で得られます。分布を描画する際には、二項分布は離散型の確率分布なのでpmf()メソッドを使います。
二項分布は試行の回数nとある事象が起こる確率pによって決まるのでしたね。離散型の確率分布なので「pmf:Probability Mass Function(確率質量関数)」であらわします。確率変数xごとの確率が確率質量関数からわかります。早速、描画してみましょう。
今回はサイコロを3回振って1の目が出る回数を考えてみましょう。試行の回数nは3ですね。1の目が出る回数は1/6となります。確率変数は3回の試行で1の目が出る回数は0~3回の4通りですね。早速やってみましょう。
# ライブラリのインポート
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import japanize_matplotlib
%matplotlib inline
# サイコロを3回振って1の目がでる回数が従う確率分布
# 試行回数
n=3
# 確率変数
x=np.arange(n+1)
# 確率質量関数
y=stats.binom(n=n,p=1/6).pmf(x)
# 描画
plt.plot(x,y,'o')
plt.vlines(x=x,ymin=0,ymax=y)
plt.grid()
plt.title('サイコロを3回振って1の目がでる回数が従う確率分布',fontsize=12)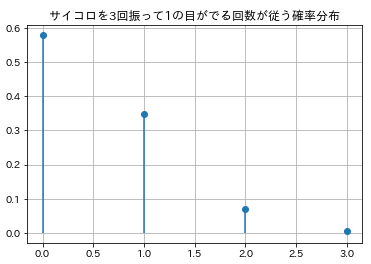
簡単ですね。3回の試行で1の目がでる回数が1回になる確率は25/72(=0.3472)でしたね。プロットを見ると、確かにそのようになっていますね。
二項分布と正規分布
繰り返しになりますが、二項分布は「 結果が成功か失敗の2つしかない試行を複数回おこなったときの成功(あるいは失敗)回数」でした。この試行回数nを無限大にしたときの分布は「正規分布」に近似します。成功する確率をpとすれば二項分布はnとpで決まるのでしたね。
※npを一定としてnを無限大にした場合はポアソン分布に近似します
正規分布は平均値$\mu$と分散$\sigma^2$で決まるのでした。nを無限大にしたときに二項分布が近似される正規分布は、平均値np, 分散npq(q=1-p)となります。
これもPythonで確認しておきましょう。まずは描画をしてみます。
list_n=(3,50,80,100)
p=1/6
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(12,6.5))
# サブプロット間の間隔を調整
plt.subplots_adjust(wspace=0.3, hspace=0.6)
# 1次元のリスト化
axes=np.ravel(axes)
for i,n in enumerate(list_n):
# 確率変数
x=np.arange(n+1)
# 確率質量関数
y=stats.binom(n=n,p=p).pmf(x)
# 描画
axes[i].plot(x,y,'o')
axes[i].vlines(x=x,ymin=0,ymax=y)
axes[i].grid()
axes[i].set_title('試行回数%d回の時の確率分布'%n)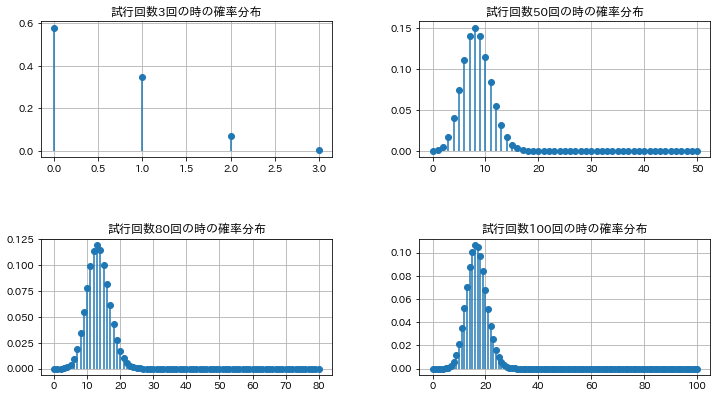
試行回数を増やすと、正規分布の形に近づいているというのがわかりますね。
▶ 複数のグラフを並べて表示する方法は以下の記事をご覧ください。
次に試行回数ごとの平均値、分散を確認しておきましょう。
for i,n in enumerate(list_n):
print('試行回数%d回の時'%n)
print('平均値は%.2f,分散は%.2f'%(stats.binom(n=n,p=p).mean(),stats.binom(n=n,p=p).var()))
print('npの値は%.2f,npqの値は%.2f'%(n*p,n*p*(1-p)))
print()
これは二項分布は(試行回数に関わらず)平均値はnp、分散はnpqとなるので、そのことが確認できたにすぎません。実際に、先ほどの確率分布のプロットに平均値np, 分散npqの正規分布を重ねるとどうなるか試してみましょう。
list_n=(3,50,80,100)
p=1/6
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(12,6.5))
# サブプロット間の間隔を調整
plt.subplots_adjust(wspace=0.3, hspace=0.6)
# 1次元のリスト化
axes=np.ravel(axes)
for i,n in enumerate(list_n):
# 確率変数
x=np.arange(n+1)
# 確率質量関数
y=stats.binom(n=n,p=p).pmf(x)
# 描画
axes[i].plot(x,y,'o',label='確率質量関数')
axes[i].vlines(x=x,ymin=0,ymax=y)
axes[i].plot(x,stats.norm(n*p,np.sqrt(n*p*(1-p))).pdf(x),label='正規分布')
axes[i].grid()
axes[i].set_title('試行回数%d回の時の確率分布'%n)
axes[i].legend()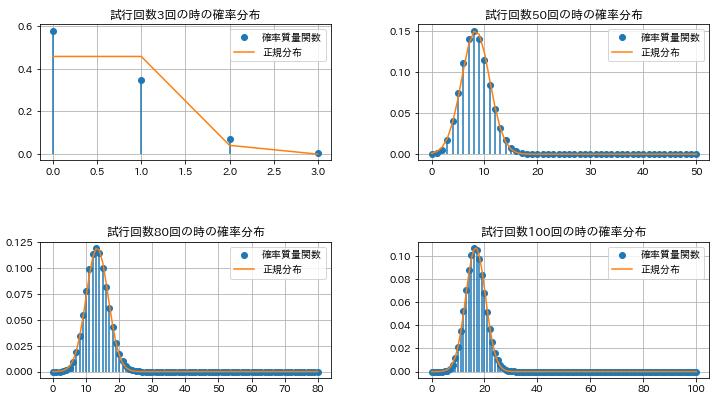
試行回数を増やすと、二項分布の確率質量関数が正規分布に近づいていく様子が見えますね。
まとめ
今回は二項分布を扱いました。二項分布とは何か、からはじめて、試行回数を増やすと正規分布に近似するところまで確認をしました。




コメント