統計学：初学者向けにPythonでt分布を扱う方法を基本から解説します

この記事はこんな方におススメです

データを分析をしたいが、どこから始めてよいかわからない方
データを仕事に活かしたいが、データの解釈の仕方がわからない方
統計学を体系的に学んだことがない、初学者の方

▶ 統計学の初学者向けに記事を書いています。はじめから読む場合は以下をどうぞ

統計学を学んだことがない初学者を対象にして、基礎から解説していきます。第一回目は記述統計を扱います。記述統計では代表値と散布度の取り扱いに分けて解説していきます。この投稿を最後まで読むと記述統計とは何かがわかり、実際にPythonでコードをかけるようになります。

はじめに

統計学を学んだことがない初学者を対象にして、基本から解説しています。今回は「t分布」について扱います。t分布は標準化をおこなった際に母分散を不偏分散で代用した時の分布です。標本サイズが30以上あれば標本正規分布として扱ってよかったですね。はじめにt分布のパラメータの確認をおこない、（近似をせずに）Pythonでt分布から直接、区間推定する方法を解説します。

t分布

t分布をWikipediaで調べてみると、次のように記載されています。

t分布（ティーぶんぷ、またはスチューデントのt分布、英: Student’s t-distribution）は、連続確率分布の一つであり、正規分布する母集団の平均と分散が未知で標本サイズが小さい場合に平均を推定する問題に利用される。
https://ja.wikipedia.org/wiki/T%E5%88%86%E5%B8%83

母集団の平均を$\mu$、分散を$\sigma$としたとき、標本の平均$\bar{x}$の標本分布は、平均$\mu$、分散$\sigma^{2}/n$となるのでした。これを標準化すると、

\[z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\]

とすると平均0、分散1の標準正規分布になるのでしたね。これをz分布と呼びます。ここで、母平均$\mu$、母分散$\sigma$が未知のときは、$\sigma$を不偏分散s’で置き換えます。

\[t=\frac{\bar{x}-\mu}{\frac{s’}{\sqrt{n}}} \]

これがt分布となります。t分布は標本サイズが大きければ（30以上）標本正規分布に近似します。標本サイズが小さいときには、t分布をみていくことになります。

t分布の特徴

t分布は自由度（degree of freedom）「n-1」のみをパラメータにとる分布です。nは標本の大きさです。平均は0で、標準正規分布と形状が似ていますが、標準正規分布に比べて裾野が広い分布となります。自由度の値を大きくすると、標準正規分布に近づいていく、という特徴があります。

裾野が広いため、同じ信頼区間で推定する場合、区間推定の「区間」は広くなります。

この標準正規分布よりも裾野が広くなる、自由度を大きくすると標準正規分布に近づく、ということをPythonで描画して試してみましょう。

ｔ分布の描画

Pythonでt分布を扱う方法を最初にまとめておきましょう。t分布を扱う際もscipyライブラリのstatsモジュールを使います。

stats.t(n-1)
※n-1は自由度

簡単ですね。早速描画していきましょう。

# ライブラリをインポート
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
%matplotlib inline

x=np.linspace(-5,5,1000)

# 標準正規分布
y=stats.norm.pdf(x)
plt.figure(figsize=(12,6))
plt.plot(x,y,label='標準正規分布',color='r',linewidth=5)
plt.ylim(0,0.42)
plt.grid()

# t分布(自由度を1,5,10,30)
for i in [1,5,10,30]:
    t=stats.t(i).pdf(x)
    plt.plot(x,t,label='t=%s'%i)
    plt.legend()
    plt.grid()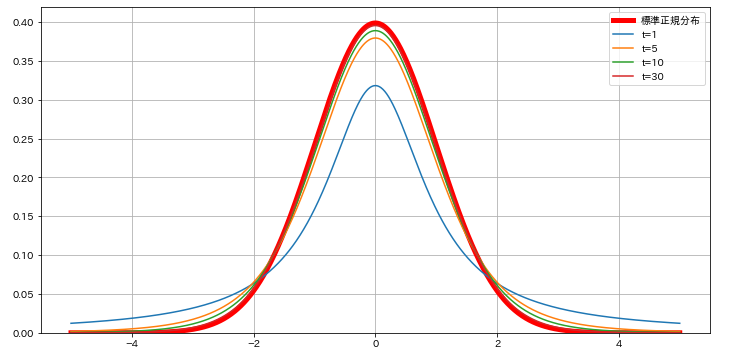

赤い太いプロットが標準正規分布です。t分布は自由度を1,5,10,30で描画してみました。t分布はいずれのプロットも裾野が標準正規分布よりも広がっています。自由度が大きくなるにつれて、標準正規分布に近づいている様子もみてとれますね。

t分布による平均値の区間推定

最初にPythonでt分布を用いて区間推定する方法をまとめておきましょう。

stats.t.interval(alpha, loc, scale, n-1)

簡単ですね。正規分布のとき「norm」としていた部分が、t分布では「t」になっているだけですね。alphaは信頼区間、locは平均、scaleは標準偏差、n-1は自由度になります。

「今回はある母集団から10000人の標本を取り出したときに、「体重」という変数の平均が62だったとします。不偏分散を100としたとき、95%の信頼区間で体重の推定をしてみましょう。せっかくなので標準正規分布で区間推定した場合と、t分布で区間推定した場合を比較してみましょう。

# 標準正規分布で区間推定
norm_min,norm_max=stats.norm.interval(0.95,loc=62,scale=0.1)
print('標準正規分布で区間推定すると体重の推定範囲は%.5fkg～%.5fkgとなります'%(norm_min,norm_max))

# 分布で区間推定
t_min,t_max=stats.t.interval(0.95,loc=62,scale=0.1,df=9999)
print('t分布で区間推定すると体重の推定範囲は%.5fkg～%.5fkgとなります'%(t_min,t_max))

信頼区間は95%とするので、alpha=0.95ですね。標本平均が62で不偏分散が100なので標本分布の分散は$\sqrt{100/10000}=0.1$、自由度は10000-1=9999を指定しています。

サンプル数が10000もあると標準正規分布でもt分布でもほとんど変わりませんね。仮にサンプル数を25としてみましょう。

# 標準正規分布で区間推定
norm_min,norm_max=stats.norm.interval(0.95,loc=62,scale=2)
print('標準正規分布で区間推定すると体重の推定範囲は%.5fkg～%.5fkgとなります'%(norm_min,norm_max))

# 分布で区間推定
t_min,t_max=stats.t.interval(0.95,loc=62,scale=2,df=24)
print('t分布で区間推定すると体重の推定範囲は%.5fkg～%.5fkgとなります'%(t_min,t_max))