統計学：初学者向けにPythonによる散布度の求め方を基本から解説します

はじめに

統計学を学んだことがない方を対象に基本から解説しています。今回は、「散布度」をPythonで求める手順を基本から解説します。範囲、四分位数、分散、標準偏差の順に扱っていきます。記事を最後まで読むことで、これらの散布度を簡単にPythonで算出できるようになります。

▶ 散布度の指標自体を確認したい場合は以下の投稿をどうぞ

統計学：初学者向けに記述統計（代表値と散布度）を基本から解説します

統計学を学んだことがない初学者を対象にして、基礎から解説していきます。第一回目は記述統計を扱います。記述統計では代表値と散布度の取り扱いに分けて解説していきます。この投稿を最後まで読むと記述統計とは何かがわかり、実際にPythonでコードを...

happy-analysis.com

散布度

まずはデータを準備しましょう。以下のコードでサンプルデータをつくってください。

# ライブラリのインポート
import pandas as pd
import numpy as np
import random
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
from scipy import stats
%matplotlib inline

# データの作成
money=[300,500,1000,1500,2000]
moneys=random.choices(money,k=12)

spend=[75,90,120,130,170,199,283]
spends=random.choices(spend,k=12)

# データフレームの作成
df_animals=pd.DataFrame({'どうぶつのなまえ':['らくだ','ねこ','ピグミーマーモセット','きりん','ぞう',
                                  'ぶた','あらいぐま','さる','ぺんぎん','くじら','いるか','しまうま'],
                      'せいべつ':['男','女','女','女','男','女','男','女','女','女','男','男'],
                      'とし':[8,3,6,9,10,21,2,3,7,2,21,34],
                      'おこづかい':moneys,
                      'つかったおかね':spends})

df_animals.head()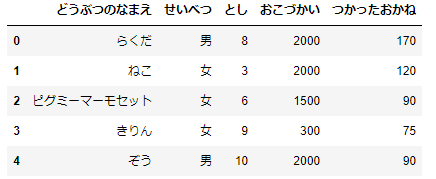

こんなデータができたら準備はOKです。では、散布度を順にみていきましょう。まずは、範囲からです。

範囲

範囲は「最大値 – 最小値」でしたね。Pythonでは代表値の場合と同様に、numpyを用いる方法、Seriesのメソッドで算出する方法があります。また、最大値・最小値もカテゴリ変数ごとの比較をするために、groupbyとともに使われることが多いことも押さえておくとよいですね。

numpyで算出するときにはnp.min(), np.max() の()の中にデータのarrayを入れます。df[‘column’].min(), df[‘column’].max() の場合は、df[‘column’]の部分でSeriesのデータが指定されていて、そのメソッドmin(), max()を利用しているので、()の中にデータを指定する必要はありません。やってみましょう。

# numpyで最小値の算出
np.min(df_animals['つかったおかね'])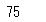

次のように算出することもできます。

# Seriesから最小値の算出
df_animals['つかったおかね'].min()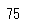

もちろん、同じ結果が返ります。次にgroupbyもみておきましょう。

# 性別による「使ったお金」の最小値・最大値の違い
df_animals.groupby('せいべつ').agg({'つかったおかね':['min','max']})

いかがでしょうか？簡単ですね。男女別の「つかったおかね」の最小値、最大値を求めることができました。

「範囲」に関しては、最小値、最大値が求まれば、「最大値」-「最小値」で求めることができます。ただ、この「範囲」は最大値と最小値を使うため外れ値に弱く、また、２つのデータしか使わないためデータのばらつきを表すには不十分ですね。

四分位数

最大値、最小値を使うため外れ値に弱い「範囲」に対して、四分位数は 「データを小さい順に並べて、データの個数で4分割したときの25%,50%,75％ の点」を使うため、「範囲」よりは外れ値に強くなります。四分位数は、numpyを使う方法とSeriesのメソッドを使う方法があります。

quantile()は分位数を求めるもので、四分位であれば0.25,0,5,0.75となるのでこれを指定しています。これを確認してみましょう。まずはnp.quantile()を使って算出してみます。

# np.quantile()を使って算出
np.quantile(df_animals['つかったおかね'],[0.25,0.5,0.75])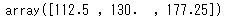

次にdf[‘column’].quantile()を使って算出してみましょう。

# df['column'].quantile()を使って算出
df_animals['つかったおかね'].quantile([0.25,0.5,0.75])

（当然ですが）このように同じ結果が返ってきます。プロットも確認しておきましょう。今回は箱ひげ図で描いてみます。箱ひげ図はmatplotlibではplt.boxplot(), seabornではsns.boxplot()で描くことができます。

実際に描いてみましょう。

# plt.boxplot()
plt.boxplot(df_animals['つかったおかね'])
plt.grid()
plt.show()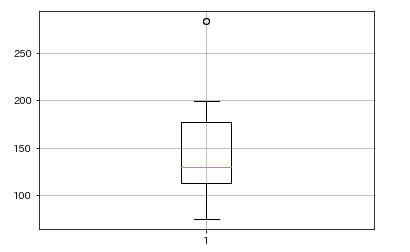

箱の底辺が第一四分位数、箱の上辺が第三四分位数、箱の中の赤線が第二四分位数（中央値）になります。そこからひげが伸びていて、ひげより上あるいは下のものは外れ値として扱われます。sns.boxplot()でも描いてみましょう。

# sns.boxplot()で描画
sns.boxplot(y=df_animals['つかったおかね'])
plt.grid()
plt.show()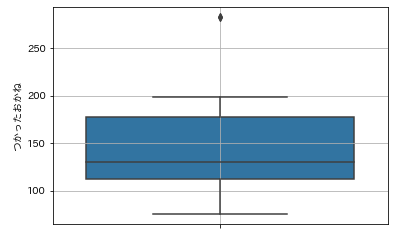

seabornの場合は、x,yという引数をとることができます。指定したデータをy方向に描きたい場合はy=df[‘column’]あるいは、y=’column’,data=dfとします。また、あるカテゴリ変数ごとに箱ひげ図を描くには、x=’カテゴリ変数’,y=’colum’,data=dfとすればOKです。これも確認しておきましょう。

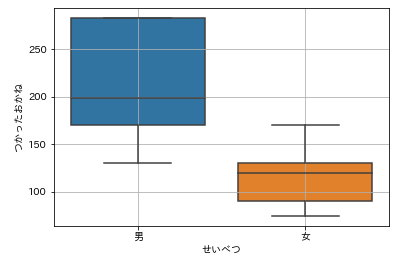
また、四分位範囲はstatsモジュールを使うと簡単に求めることができます。

これも試しておきましょう。

# 四分位範囲を四分位数から算出
stats.iqr(df_animals['つかったおかね'])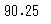

これは第三四分位数から第一四分位数を引いたものなので、np.quantile()の結果をも用いて次のように算出するっこともできます。

np.quantile(df_animals['つかったおかね'],[0.25,0.5,0.75])[2]-np.quantile(df_animals['つかったおかね'],[0.25,0.5,0.75])[0]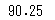

分散と標準偏差

次に分散をみていきます。四分位数ではすべてのデータを使っているわけではないため、それ以外のデータのばらつきに関しては表せていません。そこで、「平均偏差」という平均からの偏差の絶対値の平均という指標が考えられるのでしたね。ただ、「絶対値」は扱いにくいため、これを「偏差の２乗を平均」した分散が使われるのでした。

分散は、「偏差の２乗の平均」であるため、尺度がずれてしまう、という問題があります。そこで、分散の平方根をとって尺度をそろえた「標準偏差」が使われます。

これらはnumpyを使って、分散：np.var()、標準偏差：np.std()で算出することができます。

分散は以下が定義式となります。

\[s^{2}=\frac{1}{n}((x_1-\bar{x})^{2}+(x_2-\bar{x})^{2}+ \dots + (x_{n}-\bar{x})^{2})=\frac{1}{n}\displaystyle \sum_{i=1}^{n}(x_{i}-\bar{x})^{2}\]

分散にはnではなく「n-1」で割って定義される「不変分散」というものもあります。statsモジュールやSeriesのメソッドでは「不変分散」が算出されます。「分散」を算出する場合は、ここで紹介したnumpyで計算するようにしましょう。早速やってみます。

# np.var()で分散を算出
np.var(df_animals['つかったおかね'])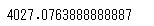

標準偏差も見ておきましょう。

# np.std()で標準偏差を算出
np.std(df_animals['つかったおかね'])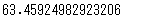

まとめ

いかがでしたか？前回学んだ散布度について、Pythonでの算出方法を解説しました。このような数値計算にはnumpyモジュールが大活躍しますね。