- データを分析をしたいが、どこから始めてよいかわからない方
- データを仕事に活かしたいが、データの解釈の仕方がわからない方
- 統計学を体系的に学んだことがない、初学者の方
▶ 統計学の初学者向けに記事を書いています。はじめから読む場合は以下をどうぞ
はじめに
統計学を学んだことがない初学者を対象にして、基本から解説しています。今回はPythonで「平均値差の検定」する方法を基本から解説していきます。平均値差の検定には「対応あり」と「対応なし」がありますが、今回扱うのは「対応なし」の場合です。まずは「対応あり・なし」とは何なのか?から解説して最後にPythonを使って実際に検定する方法を扱います。
平均値差の検定
対応ありと対応なしについて
平均値差の検定には「対応あり」「対応なし」がありますが、これが何なのかわかりますか?平均値を比較する2つの群があるときに、比較するデータ以外のすべての要素が一致している場合を「対応あり」、逆に比較するデータ以外の別の要素も異なっている場合を「対応なし」といいます。
比較する標本が同一の場合は対応あり、同一ではない場合は対応なし、ということですね。たとえば、ある小学校のクラスAとBがあって、クラスAのテストの平均とクラスBのテストの平均に差があるかどうかを検定する場合は、クラスAとクラスBという標本は対応していないので「対応なし」の検定が必要です。また、ある被験者のグループに対して新薬の効果を投薬前後で測定して比較する場合は「対応あり」となります。
具体例があるとイメージが沸きますね。今回はこの「対応なし」の平均値差の検定を扱いましょう。
対応なしの平均値差の検定
対応なしの平均値差の検定をするには次のフローチャートに従って検定方法を決定するとよいでしょう。
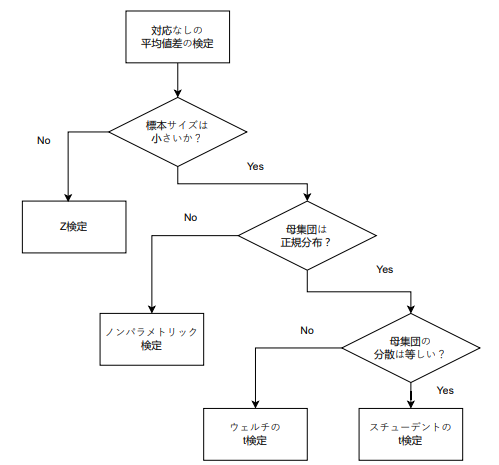
まず標本サイズが大きい場合は、標準正規分布を使うZ検定で検定することができます。これは母集団が正規分布の場合はもちろん、母集団の分布が不明であっても、標本サイズが大きいことで中心極限定理により「平均値の標本分布」が正規分布になるからです。
ただ、Z検定は近似であるため、統計ツールを用いて検定する場合はわざわざ「近似」を使う必要はないですね。なので標本のサイズによらずに「母集団は正規分布か?」の方を選択してかまいません。
次に「母集団が正規分布か?」ですが、母集団が正規分布ではない場合は「ノンパラメトリック検定」となります。これは今回は扱わないことにします。ところでパラメトリック・ノンパラメトリックというのは、母集団の分布が事前にわかっているものをパラメトリック、母集団の分布が事前にわかっていないものをノンパラメトリックといいます。分布がパラメータによって定まるので、分布がわかっていればパラメトリックというのかな。たとえば、正規分布であれば平均と標準偏差というパラメータが定まれば、分布が定まりますね。
母集団の分布が正規分布であることが仮定できれば、次は「2つの母集団の分散が等しいかどうか」で検定方法が分かれます。分散が等しいとは言えない場合は「ウェルチのt検定」、分散が等しい場合(等分散といいます)は「スチューデントのt検定」をおこないます。
通常は平均値差の検定でt検定をおこなう、といった場合は「スチューデントのt検定」を指すことが多いですが、「ウェルチのt検定」は等分散を仮定する必要がないため使いやすい検定となります。今回はこの2つの検定をする方法を見ていきましょう。
フローチャートをたどる際に、「母集団が正規分布であるか」「母集団の分散が等分散であるか」という条件がありましたが、これらはそれぞれ「正規性の検定」「等分散性の検定」があります。この検定については別途、扱うとして、今回は母集団が正規分布であることが言えた場合で、等分散性が仮定できないときにはウェルチのt検定、等分散性が仮定できたときにはスチューデントのt検定が使える、と覚えておけばよいです。
では、早速Pythonでの実装方法を見ていきましょう。
Pythonで平均値差の検定をする
準備
平均値差の検定にはscipyライブラリのstatsモジュールにあるttest_ind()を用います。t検定なのでttestということですね。さらにindは「indepent:独立」の意味ですね。「対応なし」の平均値差の検定では、標本が同一ではない、つまり独立しているのでしたね。
はじめにこのttest_ind()の使い方をまとめておきましょう。
スチューデントのt検定とウェルチのt検定の違いは、等分散を仮定できるか否かでしたね。等分散を仮定できる場合は「equal_var=True」でスチューデントのt検定、仮定できない場合は「equal_var=False」でウェルチのt検定となります。
いずれの場合も戻り値は2つあり、一つ目の戻り値がt値、二つ目の戻り値がp値となります。これはstats.ttest_ind()と入力して「Shift+Tab」を押すことで関数のdocstringを確認することができます。「Returns」の項目で以下のような記述があることからわかりますね。

問題の設定
まずサンプルを用意しましょう。これまで使ってきたseabornに用意されているtaxisを使うことにしましょう。
# ライブラリのインポート
from scipy import stats
import pandas as# ライブラリのインポート
from scipy import stats
import pandas as pd
import numpy as np
import seaborn as sns
pd.options.display.precision=1
# データセットのロード
df_taxis=sns.load_dataset('taxis')
df_taxis.iloc[0:5,0:10]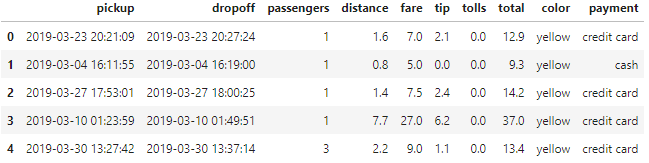
列を10列目までに絞って先頭5行のデータを表示してみました。「payment」の項目に「credit card」と「cash」の値が確認できます。「payment」にどんな値がどのくらいあるかを確認してみましょう。
# paymentのvalue_counts
df_taxis['payment'].value_counts()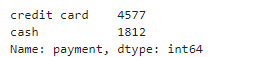
「payment」は「credit card」と「cash」の2値のようですね。それぞれ4577と1812のデータがあります。今回は支払いが「credit card」(クレジットカード)である場合と「cash」(現金)である場合で、fare(運賃)の平均に違いがあるかを検定することにしましょう
# 2群の作成
df_credit=df_taxis.query('payment=="credit card"')['fare']
df_cash=df_taxis.query('payment=="cash"')['fare']
# 平均の算出
print('クレジットで支払った場合の平均:',df_credit.mean())
print('現金で支払った場合の平均:',df_cash.mean())
クレジットで支払った場合は平均13.7、現金で支払った場合は平均11.6となりました。この平均値に差があるのかどうかを検定してみましょう。
帰無仮説と対立仮説
今回は平均値に「差があるかどうか」の検定なので両側検定となります。そのため帰無仮説、対立仮説はそれぞれ次のようになります。
- 帰無仮説
支払方法による運賃の平均値には差がない - 対立仮説
支払方法による運賃の平均値には差がある
平均値差の検定
準備が整いました。早速、Pythonで検定をしてみましょう。
# スチューデントのt検定
stats.ttest_ind(df_credit,df_cash,equal_var=True)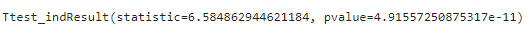
有意水準5%での検定だとすると、p値は0.05よりもかなり小さい値となるため、この統計量はめったに得られる値ではない、棄却域に入ります。そのため帰無仮説は棄却され対立仮説が成立します。つまり、今回のケースでは平均値には差がある、ということになります。
次にウェルチのt検定もみておきましょう。
# ウェルチのt検定
stats.ttest_ind(df_credit,df_cash,equal_var=False)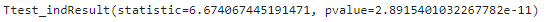
ウェルチのt検定においても棄却域に入りますね。統計ツールを使う場合は、等分散性を仮定する必要がないウェルチのt検定は使いやすいですね。
まとめ
今回は対応なしの場合の平均値差の検定をPythonで実装する方法を解説しました。平均値差の検定には「対応あり」と「対応なし」があるのでした。これは標本が同一である(対応あり)か、標本が異なる(対応なし)かでしたね。対応なしの場合には、標本が十分に大きい場合にはZ検定を利用することができます。ただ、統計ツールを使う場合には、標本が小さい場合のフローチャートに従って(近似せずに)検定するほうが一般的です。
検定方法を決定するにあたっては、まず母集団が正規分布であるかどうかを判定し(今回の記事では扱っていません)、正規分布として扱うことができなければノンパラメトリック検定(今回の記事では扱っていません)をおこない、正規分布として扱うことができるならばパラメトリック検定をおこないます。
次に母集団の分散が同じと仮定できるのであれば、スチューデントのt検定、仮定できなければウェルチのt検定をおこなう、という流れでしたね。



コメント