統計学：初学者向けにPythonで比率差の検定をする方法を基本から解説

 

はじめに

統計学を学んだことがない初学者を対象にして、基本から解説しています。今回はPythonで「比率差の検定」する方法を基本から解説していきます。前回、統計ツールを利用しない前提で、比率差の検定をする方法を解説しました。かなり多くのステップを経てやっと「検定」できた、という感じでしたが、統計ツールを使うとこれらが一瞬でできてしまいます。早速やっていきましょう。

比率差の検定

比率差の検定には、statsmodelsライブラリを用います。はじめにこの使い方をまとめておきましょう。モジュール名にもあるように、「比率差の検定」のことを「z検定」というので、覚えておくとよいですね。

引数を確認しておきましょう。countは標本で実際に観察できた数です。nobsは標本の大きさ、つまりデータの数です。比率差の検定なのでcount,nobsはそれぞれリストで指定します。このcount/nobsで比率となるわけですね。alternativeは対立仮説です。ここで両側検定（two-sided）なのか片側検定（下側検定:smaller、上側検定:larger）なのかを指定します。

count,nobsに入れる順番と、alternativeの指定を間違えると、まったく意味をなさないので注意しましょう。標本1と標本2があったとして、標本1の観測数をx1、標本の大きさをn1とします。同様に標本2の観測数をx2、標本の大きさをn2とします。このとき、標本1の比率はx1/n1、標本2の比率はx2/n2で、比率の差はx1/n1-x2/n2となります。両側検定のときには迷いようがないですが、片側検定の時にはsmallerなのかlargerなのか、注意してください。x1/n1<x2/n2を示したいのであれば、x1/n1-x2/n2は0より小さくなってほしいので、下側の片側検定になります。つまり、smallerになります。

早速やってみましょう。

前回の記事で例にした、メールの開封率で考えましょう。標本１では開封数が100、到達数が832、標本2では開封数が150、到達数が965とします。標本2の方が標本1よりも開封率が高いことを示したい、とします。すると、これは下側の片側検定になりますね。

# ライブラリのインポート
from statsmodels.stats.proportion import proportions_ztest

# 検定
proportions_ztest([100,150],[832,965],alternative='smaller')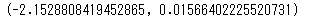

値が２つ返ってきてますね。前者が検定統計量、後者がp値となります。まず、検定統計量を見ると、「-2.15」です。5%の有意水準で考えると、この値は-1.64より小さいので棄却域に入っていますね。念のためp値をみると、0.015となり0.05より小さい値なので、帰無仮説は棄却されます。

前回、あれだけ多くのステップを経てやっと検定したものが、Pythonを使うとたった1行のコードで検定できました。

まとめ

いかがでしたでしょうか？今回はPytyonを用いて比率差の検定をする方法を解説しました。統計ツールを使うと、こんなに簡単に検定をすることができます。比率差の検定では、これまで使っていたscipyライブラリではなく、statsmodelsというライブラリを使うので混同しないようにしましょう。