- データを分析をしたいが、どこから始めてよいかわからない方
- データを仕事に活かしたいが、データの解釈の仕方がわからない方
- 統計学を体系的に学んだことがない、初学者の方
▶ 統計学の初学者向けに記事を書いています。はじめから読む場合は以下をどうぞ
はじめに
統計学を学んだことがない初学者を対象にして、基礎から解説しています。今回は「推定」について扱います。統計学は大きく2つに分けると「記述統計」と「推測統計」に分かれます。「推測統計」は「推定」と「検定」に分かれます。さらに「推定」には「点推定」と「区間推定」があります。今回は特に、「区間推定」をとりあげます。比率の区間推定、平均の区間推定の順にみていきましょう。
推測統計
冒頭にも記載しましたが、「推測統計」は大きく「推定」と「検定」にわかれます。「推定」についてはこれまでも触れていますが、「推定」「検定」ぞれぞれについて簡単に整理すると
- 推定
母集団から標本をとって、標本の統計量から母集団の特性を推測する - 検定
「2つの標本があったときに、それぞれの母集団の統計量が同じであるか?」や「ある標本の母集団は正規分布といえるか?」などを判定する
のようになります。今回は「推定」について進めていきましょう。
推定
推定は「点推定」と「区間推定」にわけられます。これは文字通りなのですが、;
- 点推定
1つの値で推定すること - 区間推定
ある区間をもって推定すること
です。点推定については、前回扱ったように、「平均の標本分布の平均」が「母平均」となる、などのように1つの値で推定するものですね。今回は、区間推定を扱っていくことにしましょう。
比率の区間推定
ここで比率というのは、あるカテゴリ変数の値ごとの数の比のことです。男女の比や裏表の比などです。「比率の区間推定」というのは、標本の比率から母集団の比率を区間をもって推定すること、です。またもう一つ特徴的なのは区間推定では区間とともに確度を示します。この区間のことを「信頼区間」といいます。
区間推定は標本推定量の標本分布を使って推定します。「比率の区間推定」であれば、標本の比率の標本分布を使います。(確率的に決まる)標本によって、計算される統計量が決まるので、統計量は確率的に決まる確率変数になるのでしたね。そのため、標本分布を考えるのです。
ところで、成功確率がpである試行をn回行うときに成功する回数をXとすると、Xは二項分布B(n,p)に従うのでした。このpが母比率に対応します。(p=X/n)
▶ 二項分布を復習する場合は、こちらの記事をどうぞ
二項分布はnが十分大きい時には、正規分布に近似できるので、平均np、分散npqの正規分布に近似できることになります。
※母比率は二項分布に従うのではなく、Xが二項分布に従う点に注意。
これは、nが十分に大きいときに、
- 確率変数Xは平均np、分散npqの正規分布に近似できる
- 確率変数X/nは平均p、分散pq/nの正規分布に近似できる(比率で考えた場合)
ということです。
次に、標本分布において、標本比率がどのくらいの確率で起こるかを考えるにあたり、正規分布を標準化することを考える。※こうすることで毎回同じ形の分布(標準正規分布)となるので、決まった作業で区間を考えることができる。
▶ 標準化について復習する場合は、以下の記事を合わせてお読みください。
すると、95%の信頼区間は変換後の確率変数が-1.96~1.96の間に入ることになります。Pythonで区間推定する際の手順も確認しておきましょう。nが十分大きい場合には二項分布に近似できるので、statsモジュールのbinomを使います。
- stats.binom.interval(alpah, n, p)
binomは二項分布でしたね。intervalは区間推定のメソッドです。引数のalphaで信頼区間を決めます。95%信頼区間の場合は0.95と指定します。nは試行回数(比率の場合は標本の大きさ)、pは成功確率(比率の場合は標本比率)です。返ってくるのは、(比率の推定であっても)成功回数となります。比率そのものが返ってくるわけではなく、比率X/nに対して、Xの値が返ってくることに注意しましょう。早速やってみましょう。
今回はある母集団から10000人の標本を取り出したときに、「性別」という変数の男性の比率が全体の70%だったとします。このとき、95%の信頼区間で男性比率の推定をしてみましょう。
# ライブラリのインポート
from scipy import stats
import numpy as np
# 95%の信頼区間で男性比率を区間推定
stats.binom.interval(alpha=0.95,n=1000,p=0.7)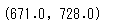
返り値は、標本1000に対して95%の信頼区間に入るときの男性の人数となります。95%の信頼区間では671人~728人の間となる、ということですね。つまり比率で考えると、671/1000=67.1%から、728/1000=72.8%ということですね。Pythonで計算する場合は、正規分布への近似→標準化して標準正規分布から計算、という作業を行う必要はありません。統計ツールでは近似する必要はなく、直接計算してくれます。
平均値の区間推定
次に平均値の区間推定をみていきましょう。母平均の推定量は「標本平均」でしたね。なので、標本の平均値から母集団の平均値を推定する、ことになります。
比率の区間推定の場合と同様に、「標本の平均の標本分布」を考える。この「標本の平均の標本分布」は、平均$\mu$、分散$\sigma^2/n$となる。($\mu$は母平均、$\sigma^2$は母分散)この分布は正規分布になるとは限らないが、標本サイズが大きいときには正規分布に近似(中心極限定理)できる。「標本サイズが大きい」の目安は5以上と考えておけばよい。
次に標本分布において標本平均がどのくらいの確率で起こるかを考えるにあたり、正規分布を標準化することを考える。※こうすることで毎回同じ形の分布(標準正規分布)となるので、決まった作業で区間を考えることができる。
但し、母分散$\sigma^2$がわかっていないためこれを不偏分散s’で代用する。
\[ s’^2=\frac{1}{n-1}\displaystyle \sum_{i=1}^{n}\]
これは標本で計算することができる。厳密には母分散を標本の不偏分散に置き換えたことにより標準正規分布にはならない。但し、標本サイズが大きい時には標準正規分布に近似することができる。このときの「標本サイズが大きい」の目安は大体30くらいだそうです。
最後にPythonで平均の区間推定をする場合の手順を確認しておきましょう。これまで見てきたように正規分布を使って平均の区間推定をするので、statsモジュールのnormを使います。
- stats.norm.interbal(alpha, loc, scale)
intervalやalphaは比率の区間推定のところでも触れたようにintervalは区間推定のメソッドです。これを指定するにあたり、alphaで何%の信頼性区間とするかを指定します。loc, scaleは正規分布のパラメータでlocが標本平均、scaleが標本分布の標準偏差となる。上で説明したように母分散がわかっていないから不偏分散を使います。
今回はある母集団から1000人の標本を取り出したときに、「体重」という変数の平均が62だったとします。不偏分散を100としたとき、95%の信頼区間で体重の推定をしてみましょう。
データの数nは10000ですね。信頼区間を95%とするとのでalpha=0.95となります。標本の平均の標本分布はデータの数が大きければ平均$\mu:母平均、分散\sigma^2/n$の正規分布に近似できるのでしたね。平均loc=62、標準偏差は母分散がわかっていないので不偏分散で代用します。すると、$s’^2/n$の平方根は100/10000の平方根なので0.1となります。
# 95%の信頼区間で体重の区間推定
stats.norm.interval(0.95,62,0.1)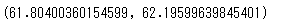
つまり体重の母平均は95%の信頼区間で61.8~62.2となります。
まとめ
今回は「区間推定」を扱いました。「比率の区間推定」「平均の区間推定」の順にみてきましたが、どちらも同じような考え方を適用していましたね。
まず標本の比率あるいは、標本の平均の標本分布を考えます。データが一定以上あれば標本分布が正規分布に近似できるので、これを標準化して「標準正規分布」として考えることで、95%信頼区間なら標準化したZが-1.96~1.96の間に入る、として計算するのでしたね。





コメント