統計学：初学者向けにPythonで不偏分散を算出する方法を解説

はじめに

統計学を学んだことがない方を対象に基本から解説しています。今回は、「不偏分散」をPythonで求める手順を基本から解説していきます。母数を推定するのに使う統計量を「推定量」と呼ぶのでしたね。推定量の中には、不偏性を持つもの/持たないものとがあります。標本分散は不偏性を持たないため、母分散の推定量としては「不偏分散」を使います。早速、確認していきましょう。

不偏分散をもとめる

Pythonでの不偏分散の求め方を最初にまとめておきましょう。scipyライブラリのstatsモジュールを使う方法とnumpyライブラリを使う方法とがあります。

確認しておきましょう。まずはデータの準備をしましょう。

# ライブラリのインポート
import pandas as pd
import numpy as np
from scipy import stats
import seaborn as sns

# データセットの読み込み
_=sns.load_dataset('taxis')
df=_.iloc[:,0:10]
df.head()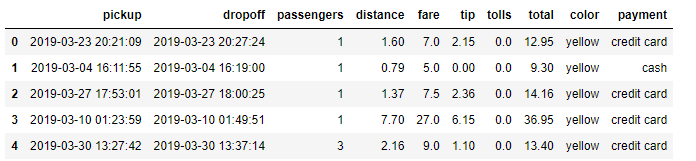

distanceで不偏分散を求めてみましょう。まずはstatsモジュールで求めてみます。

# statsモジュールで不偏分散を求める
stats.tvar(df['distance'])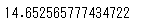

次にnumpyで求めてみましょう。

# numpyで不偏分散を求める
np.var(df['distance'],ddof=1)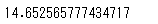

一致しますね。numpyではddofを指定しない場合は普通の分散が算出されるので注意しましょう。

不偏分散の平方根を求める

同じように不偏分散の平方根についてもはじめにまとめておきましょう。

不偏分散の場合と同じような感じですね。確認しましょう。

# statsモジュールで「不偏分散の平方根」を求める
stats.tstd(df['distance'])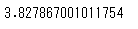

次にnumpyで求めてみましょう。

# numpyで「不偏分散の平方根」を求める
np.std(df['distance'],ddof=1)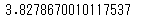

こちらもちゃんと一致しますね。これは不偏分散の平方根を直接計算しても得られます。

# 不偏分散から、直接「不偏分散の平方根」を求める
np.sqrt(stats.tvar(df['distance']))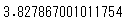

これもちゃんと一致しますね！

不偏性の確認

最後に不偏性を確認しておきましょう。これは、また母集団をみたてて、そこから標本を抽出することを繰り返せばよいですね。やってみましょう。母集団から100個のデータを抽出して標本として、分散・不偏分散を求める作業を1000回繰り返してみましょう。

# 100個のデータを抽出して分散・不偏分散を計算する作業を1000回繰り返す
var_list=[]
tvar_list=[]

n=1000
data=100

for i in range(n):
    _=df.sample(data)
    var_list.append(np.var(_['distance']))
    tvar_list.append(np.var(_['distance'],ddof=1))

これで標本の分散・不偏分散の1000回分のデータを取得する音ができました。不偏性は「平均的に」母数と一致することなので、母分散とこれらの1000個の標本から計算した分散・不偏分散の平均値を比較してみることにしましょう。

# 標本の分散の平均と標本の不偏分散の平均と、母分散を比較する
print('標本の分散の平均は%.2f'%np.mean(var_list))
print('標本の不偏分散の平均は%.2f'%np.mean(tvar_list))
print('母分散の値は%.2f'%np.var(df['distance']))

この例では、ちゃんと不偏分散のほうが母分散に近い値となっていますね。

まとめ

今回はPythonによる不偏分散の求め方の説明から初めて、実際に「不偏分散は不偏性があるか」の確認をしました。この確認は、母集団とみたてたデータセットからランダムにデータを抽出するという作業を繰り返して、実際に抽出したデータ（標本）の分散・不偏分散を計算して、それらの平均と母分散を比較数ことでおこないました。