統計学：初学者向けに母数の推定を基本から解説

この記事はこんな方におススメです

データを分析をしたいが、どこから始めてよいかわからない方
データを仕事に活かしたいが、データの解釈の仕方がわからない方
統計学を体系的に学んだことがない、初学者の方

はじめに

統計学を学んだことがない初学者の方を対象にして基礎から解説しています。今回は「母数の推定」について基本から解説していきます。推測統計の興味の対象は「母集団」でしたね。母集団を調査することはできないから「標本」から「母集団」を推定します。「母集団」の統計量のことを母数と表現するので、「母数の推定」をすることになります。

母数の推定

母集団を直接調査できないので「標本」から「母集団」を推定します。その際、「標本」の統計量（つまり「標本統計量」）から母集団の統計量（つまり母数）を推定できないか？と考えます。統計量によっては単純に、標本統計量からそれに対応する母数を推定するよりも、適切な統計量がある場合もあります。その辺も整理していきましょう。

推定量

母数の推定に使う統計量を「推定量」と呼びます。母数ごとに利用する推定量は決まっています。以下の対応があります。

母数	推定量
母平均値$\mu$	標本平均値$\bar{x}$
母比率$\pi$	標本比率$p$
母相関係数$\rho$	標本相関係数$r$
母分散$\sigma^2$	不偏分散$s’^{2}$
母標準偏差$\sigma$	不偏分散の平方根$s’$

標本分布

標本統計量から母数を推定するときに、「標本分布」を考えます。この「標本分布」は標本の分布ではない、ので注意してください。順に説明していきましょう。

「標本」は母集団から無作為に抽出するものなので、確率的に変動します。そのため、標本の統計量である「標本統計量」も確率的に変動します。つまり、確率変数となります。「標本統計量」が確率変数であれば、その背後には確率分布が存在するはずです。子の分布のことを「標本分布」といいます。つまり、標本分布は標本統計量が従う確率分布のこと、です。

標本統計量が母数の推定に適しているかはどのように考えたらよいでしょうか？それには「不偏性」を先に説明することにしましょう。

不偏性

推定量が平均的に母数と一致する場合、その推定量は「不偏性がある」といいます。つまり不偏性がある場合は「平均的に」母数と一致するので、標本分布の統計量を算出すればよい、ということになります。このような不偏性のある推定量を「不偏推定量（unbaiased estimator）といいます。

たとえば、「平均の標本分布」の平均は母平均と一致します。つまり不偏性があります。

平均の標本分布

母集団（平均$\mu$、標準偏差$\sigma$）からn個のデータが入った標本を無限回取ったとする。各標本から「標本平均」を計算してその値を$\bar{x_1},\bar{x_2},,,\bar{x_\infty}$を計算すると、この分布が「平均の標本分布」となる。平均の標本分布の平均は、母集団の平均と一致するので$\mu$となります。平均の標本分布の分散は母分散をnで割った値$\sigma^2/n$となる。

これをPythonにより確かめてみましょう。まずはデータを準備します。

# ライブラリのインポート
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import japanize_matplotlib
%matplotlib inline

# データセットの読み込み
_=sns.load_dataset('taxis')
df=_.iloc[:,0:10]
df.head()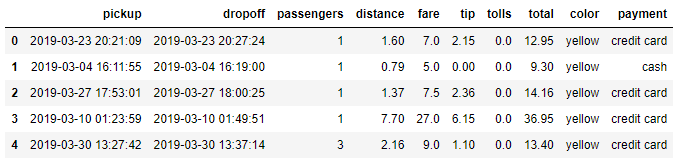

このdfを母集団とみたてることにしましょう。ここでここからデータ数が100個となる標本を取り出す、という作業を500回繰り返すことにします。このときの「標本平均値の平均」「標本平均値の分散」をみてみることにしましょう。今回は「distance」のcolumnで試すことにします。

今回はdfを母集団と見立てるので、母平均$\mu$、母分散$\sigma$を直接計算することができます。これを求めておきましょう。

# 母平均
mu=df['distance'].mean()
# 母分散
var=df['distance'].var()

print('母平均は%.2f'%mu)
print('母分散は%.2f'%var)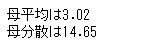

次に、平均の標本分布をみてみましょう。母集団から500個のデータを抽出して標本をつくる、という作業を100回繰り返します。このとき、各標本で標本平均を求めてこれをリストにしておけば、「標本平均の平均」、「標本平均の分散」は簡単にもとめられますね。

# 標本分布（標本平均の分布）
list_mean=[]
n=100
data=500

for i in range(n):
    # データの個数data個の標本を作る
    tmp=df.sample(data)
    tmp_mean=tmp['distance'].mean()
    # 標本平均のリスト
    list_mean.append(tmp_mean)

# 平均の標本分布の「平均・分散」    
print('平均の標本分布の平均は%.2f'%np.mean(list_mean))
print('平均の標本分布の分散は%.2f'%np.var(list_mean))

まず、母平均と「平均の標本分布の平均」を比較してみましょう。母平均は3.02、「平均の標本分布の平均」は3.02となります。確かに母平均の推定値は標本平均となっているようですね。
※ここでいう標本平均は、取り出した標本の平均が従がう確率分布の平均のことです。

分散についてはどうでしょうか？（標本）平均の標本分布の分散は母分散をnで割った値$\sigma^2/n$でしたね。これを確かめてみましょう。母分散が 14.65なのでデータ数500で割ると0.029、「平均の標本分布の分散」は3.02となります。かなり近い値となることが確認できますね。

まとめ

今回は母数の推定に使う推定量について解説しました。母数の推定に使う統計量のことを「推定量」と呼ぶのでしたね。そして、推定量が平均的に母数と一致する場合、その推定量は「不偏性がある」といいます。「不偏性がある」推定量は母数を推定しやすくて有用ですね。母平均の推定には、標本の平均値が使われます。標本自体が確率的に変動するので、標本の平均値も確率的に変動する、確率変数といえます。標本の平均が従う確率分布を「標本分布」というのでした。

標本平均は不偏性があるため、（標本）平均の標本分布から平均を求めれば母平均が推定できる、というわけですね。少しややこしいですが、最後にPythonでこれらを確かめるところまでを扱いました。