統計学：初学者向けにPythonで累積分布関数を実装する方法を解説します

はじめに

統計学を学んだことがない初学者を対象にして基礎から解説しています。確率変数が連続変数である場合、確率密度関数によって確率密度を表します。「区間」を指定すると確率が定まるのでしたね。確率密度関数を区間で積分すれば確率を求められますが、「累積分布関数」を使うともっと簡単に確率を求めることができます。今回はPythonでこれを確かめていきましょう。

Pythonによる実装

では、Pythonで実装していきましょう。今回もstatsモジュールを使います。分布は「正規分布」を使うことにしましょう。まずはライブラリをインポートして、確率変数を定義しましょう。

# ライブラリのインポート
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
%matplotlib inline

# 確率変数の各値
x=np.linspace(-5,5,1000)

まずは必要なライブラリのインポートや描画のための設定をします。その後、確率変数の値をnp.linspace(-5,5,1000)で定義しています。これは、-5から5までの間で1000個の点を作ります。

正規分布の確率密度関数

早速、正規分布の確率密度関数を書いていきましょう。正規分布はnorm()でしたね。locで平均、scaleで標準偏差を指定することができます。loc=0,scale=1を指定すれば標準正規分布になります。この標準正規分布に、pdf()メソッドを指定すればよいですね。

# 正規分布の確率密度関数を指定
y1=stats.norm(loc=0,scale=1).pdf(x)

# 描画
plt.plot(x,y1)
plt.grid()
plt.title('確率密度関数')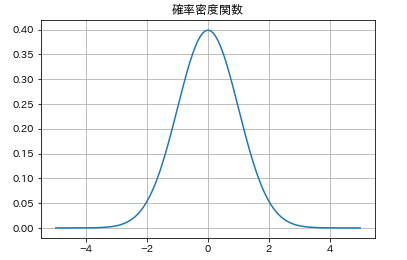

正規分布の累積分布関数

次に累積分布関数を描いてみましょう。こちらは、先ほどpdf()を指定した個所をcdf()に書き換えるだけです。

# 正規分布の累積分関数を指定
y2=stats.norm(loc=0,scale=1).cdf(x)

# 描画
plt.plot(x,y2)
plt.grid()
plt.title('累積分布関数')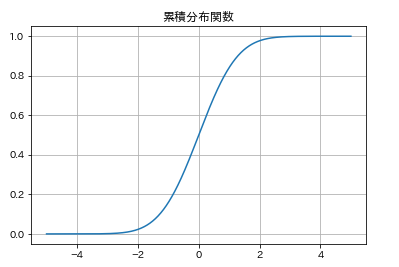

確率密度関数を負の無限大からある値まで積分したものが、累積分布関数である値を指定した時の値になっているのが感覚的にわかるでしょうか？たとえば、確率密度関数を負の無限大から-3までの区間が表す面積はほぼ0に見えますね。累積分布関数でも-3のあたりでは0になっています。

一方で、確率密度関数で負の無限大から0まで積分すると、ちょうど真ん中なので（全面積が1なので）0.5になります。累積分布関数で0を指定するとどうでしょう？これも0.5になってそうですよね。

生存関数（SF:Survival Function）

1-cdf(x)であらわされる関数を「生存関数」といいます。累積分布関数が「確率密度関数を負の無限大からxまで積分したもの」で「x以下になる確率」を表すのに対して、生存関数は「確率密度関数をある値xから無限大まで積分したもの＝1-cdf(x)」で「x以上になる確率」を表します。この生存関数はsf(x)メソッドで与えられます。確かめてみましょう。

# 正規分布の生存関数を指定
y3=stats.norm(loc=0,scale=1).sf(x)

# 描画
plt.plot(x,y3)
plt.grid()
plt.title('生存関数')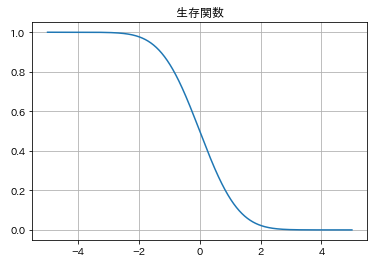

累積分布関数を左右対称にしたものとなっているのがわかりますか？これは1-cdf(x)でも描画することができます。これも確認しておきましょう。

# 1-cdf(x)を描画
y4=1-y2

# 描画
plt.plot(x,y4)
plt.grid()
plt.title('1-cdf(x)')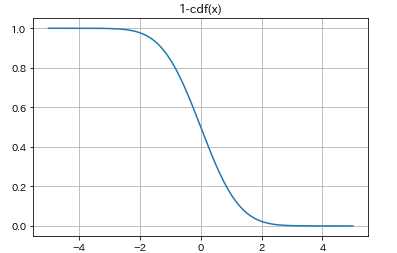

一致してますね。

まとめ

今回は確率密度関数を積分しなくても簡単に確率を求めることができる、「累積分布関数」をPytonで実装する方法を扱いました。また、ある値x以上である確率を表す「生存関数」の確認をおこないました。累積分布関数は、区間の確率を簡単に求められるだけではなく、複数の分布の差異を視覚的に表すことにも利用されます。