統計学：初学者向けに相関係数について基本から解説します

この記事はこんな方におススメです

データを分析をしたいが、どこから始めてよいかわからない方
データを仕事に活かしたいが、データの解釈の仕方がわからない方
統計学を体系的に学んだことがない、初学者の方

▶ 統計学の初学者向けに記事を書いています。こちらの記事もお読みください。

統計学を学んだことがない初学者を対象にして、基礎から解説していきます。第一回目は記述統計を扱います。記述統計では代表値と散布度の取り扱いに分けて解説していきます。この投稿を最後まで読むと記述統計とは何かがわかり、実際にPythonでコードを...

はじめに

統計学を学んだことがない方を対象に基本から解説しています。今回は、「相関係数」を基本から解説します。連続する変数間の相関関係の強さを表すものとして「共分散」がありますが、これは変数ごとに大きさがまちまちとなり、単純に比較できません。そこで、相関の強さを標準化した「相関係数」が使われます。今回の記事を読めば、実際にPythonで相関係数を求めることができるようになります。

2変数間の相関関係

共分散

連続変数の相関関係の強さは「共分散」によってあらわすことができます。共分散$S_{xy}$の定義は以下となります。

\[共分散の定義式：S_{xy}=\frac{1}{n}\displaystyle \sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})\]

１変数のばらつきの指標である「分散（$s^{2}$）」の定義式が以下であったことを考えると、2変数間のばらつき（相関の強さ）の指標となる共分散がこのような式になるのは想像しやすいですね。

\[分散の定義式：s^{2}~\frac{1}{n}\displaystyle \sum_{i-1}^{n}(x_{i}-\bar{x})^{2}\]

共分散が2変数間の相関の強さを表すものであったとしても、選ぶ2変数によって大きさや尺度がまちまちになるため、比較ができません。

相関係数（correlation coefficient）

そこで、これらを比較できるように標準化したものが「相関係数）となります。「相関係数」の取りうる値は、「-1」～「1」となります。Pythonで実際に相関係数を求めてみましょう。

相関係数の算出

サンプルデータ

まずはサンプルデータを準備しましょう。次のコードでサンプルデータを作成しましょう。

# ライブラリのインポート
import pandas as pd
import numpy as np
import random
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
from scipy import stats
%matplotlib inline

# データの作成
money=[300,500,1000,1500,2000]
moneys=random.choices(money,k=12)

spend=[75,90,120,130,170,199,283]
spends=random.choices(spend,k=12)

# データフレームの作成
df_animals=pd.DataFrame({'どうぶつのなまえ':['らくだ','ねこ','ピグミーマーモセット','きりん','ぞう',
                                  'ぶた','あらいぐま','さる','ぺんぎん','くじら','いるか','しまうま'],
                      'せいべつ':['男','女','女','女','男','女','男','女','女','女','男','男'],
                      'とし':[8,3,6,9,10,21,2,3,7,2,21,34],
                      'おこづかい':moneys,
                      'つかったおかね':spends})

df_animals.head()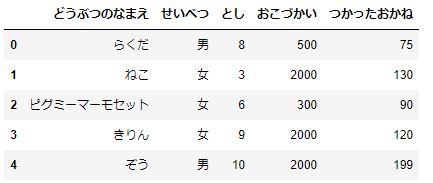

相関係数の算出

Pythonでは相関係数（相関行列）をnumpyを使って、２変数の場合はnp.corrcoef(xarray,yarray)で、それ以上の変数の場合はnp.corrcoef(array)で算出することができます。また、データフレームのcorr()メソッドを使って算出することもできます。

np.corrcoef(xarray,yarray)
np.corrcoef(array)
df.corr()

実際にやってみましょう。まずは2変数の場合です。

# np.corrcoef()で算出
np.corrcoef(df_animals['とし'],df_animals['おこづかい'])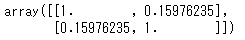

このように「とし」と「おこづかい」の間の相関係数は「0.159・・・」とわかります。3変数以上の場合は、np.stackを使って１つのarrayにします。こちらも確認しておきましょう。

# 3変数の場合の相関行列
array=np.stack([df_animals['とし'],df_animals['おこづかい'],df_animals['つかったおかね']],axis=0)
np.corrcoef(array)

このように簡単に求めることができます。一つ目の変数「とし」と２つ目の変数「おこづかい」の相関係数は0.159・・・となり、先ほどの値と一致しますね。

既にデータがデータフレームになっている場合は次のようにすると、一発で相関行列を求めることができます。

# データフレームから直接
df_animals.corr()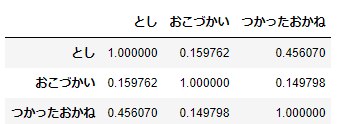

これだと、どの変数間の相関係数であるかがわかりやすいですね。１つ注意点ですが、データフレームにはこの他にも列項目がありましたが、相関係数は連続変数間の相関の強さを表すものであるためカテゴリ変数は表示されません。

こういった行列で値を表すものに関しては、ヒートマップを描くとわかりやすい。これはseaboanを使うと簡単に描画できます。

sns.heatmap(df.corr())

やってみましょう。先ほど求めた、相関行列df_animals.corr()をsns.heatmap()の中にいれるだけです。

# ヒートマップの描画
sns.heatmap(df_animals.corr())

色によって相関の強さが一目でわかりますね。色を指定したり、相関係数の値を表示させることもできます。

# ヒートマップの描画2

sns.heatmap(df_animals.corr(),cmap='coolwarm',annot=True)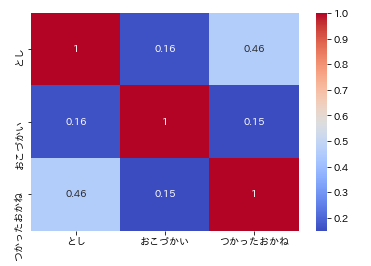

まとめ

いかがでしたか？今回は2変数間の相関の強さを表す相関係数を扱いました。2変数間の相関をあらわす指標としては「共分散」が考えられますが、これは標準化されていない値であるため比較ができないのでした。そこで、「共分散」を標準化した「相関係数」を導入したのでしたね。

Pythonでは、numpyモジュールを用いてnp.corrcoef()で相関行列を算出することができることを確認しました。データがデータフレームとしてすでにある場合は、df.corr()を使うと便利でした。

また、これらの相関行列はヒートマップによる可視化を行うと、視覚的に相関の強さをとらえることができて便利でしたね。