- 時系列データの処理の仕方を知らない、または、基本から学びたい方、
- 時系列データを扱ったことがあるが、体系的に整理できていないので、学びなおしたい方
▶ 時系列データ解析のやり方を基本から解説しています。以下の記事もどうぞ。



はじめに
前回に引き続き時系列データ解析を扱います。前回は時系列データ解析のモデルを整理しました。今回はサンプルデータを用いて、データが定常であるかの確認や、非定常データの加工など、実際に時系列データを前にしたときにおこなう手順を説明し、モデル構築をやっていきましょう。最後に構築したモデルで予測をおこない、実際のデータとの比較までおこないます。基本から丁寧に説明していきます。
データの準備
今回はR言語で組み込みデータセットとして提供されている、飛行機の乗客数のデータを扱うことにしましょう。Pythonにはデータセットとして組み込まれていないようですが、検索すればcsvで提供してくれているサイトが見つかります。早速データを確認していきましょう。
# ライブラリのインポート
import pandas as pd
# データの読み込み
data=pd.read_csv('C://python//data/AirPassengers.csv')
data.head()
普通に読み込むと、「Month」と「#Passengers」という列をもったデータですね。「Month」の部分が時を表しているので、これをインデックスにしましょう。set_indexで指定してもよいですが、読み込み時にindex_colでインデックスに使用する列を指定することができます。また、parse_dates=Trueを指定しておくと、読み込み時にDateTime型に変換してくれます。
# データの読み込み(インデックスを指定して、DateTime型で読み込み)
data=pd.read_csv('C://python//data/AirPassengers.csv',index_col='Month',parse_dates=True)
data.head()
列名が「#Passengers」では扱いにくいので「passengers」に変えておきましょう。
# 列名の変更
data.columns=['passengers']
data.head()
時系列データ解析の手順
時系列データ解析を始めるまでに、手順を確認しておきましょう。大まかな流れは次のようになります。
- データの読み込み
- データの理解・可視化
- 周期の把握
- パラメータの決定
- モデルの構築
- 予測と評価
データは各月の飛行機の乗客数という単純なデータでした。ここでは、可視化から始めてみましょう。
データの可視化
時系列データの可視化は簡単ですね。既にインデックスにDatetime型としているので、plot()に「passengers」の列を指定するだけです。
# ライブラリの読み込み
import matplotlib.pyplot as plt
%matplotlib inline
# 可視化
plt.figure(figsize=(16,8))
plt.plot(data['passengers'])
plt.title('飛行機の乗客数の推移',fontsize=20)
plt.xlabel('年月',fontsize=15)
plt.ylabel('乗客数',fontsize=15)
plt.grid()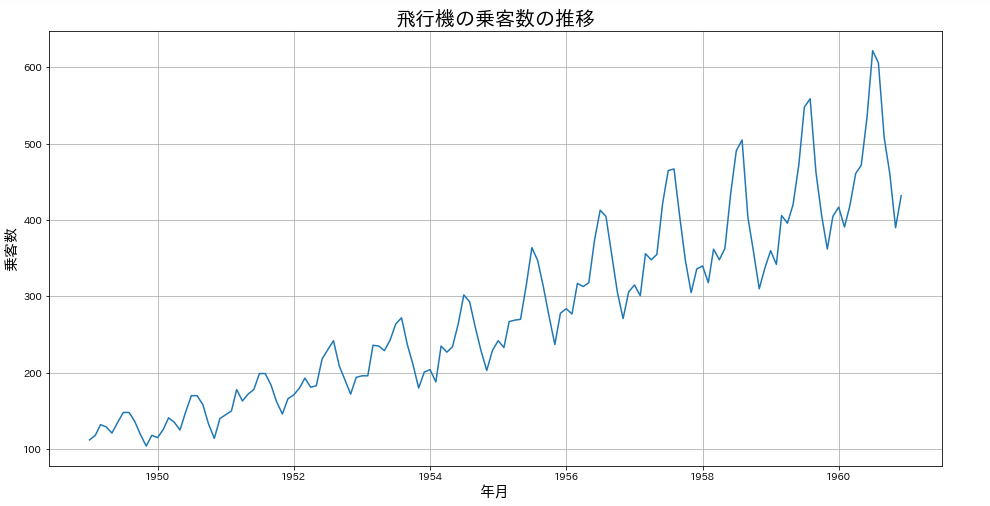
こうして可視化するだけでもわかることがありますね。
- 乗客数は毎年増えている
- 周期的な変動(12か月?)が見られる
周期の把握
ここでは「自己相関係数」と「偏自己相関係数」を使って周期を把握しましょう。まずは、「自己相関係数」「偏自己相関係数」とは何かを確認していきましょう。
例えば今日と一日前に「正」の自己相関があれば、「一日前に多ければ、今日も多い」のように解釈できます。
但し、「今日と一日前が似ている」、と考えた時、「一日前と二日前も似ている」、と考えられます。すると、「今日と二日前が似ているのか?」よくわからなくなります。そこで、注目している観測点以外の要因を無視して、「今日と一日前のみの関係」を表す、偏自己相関係数を合わせて確認します。
# 自己相関のグラフ
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(data.passengers, lags=40, ax=ax1)
# 偏自己相関のグラフ
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(data.passengers, lags=40, ax=ax2,method='ywmle')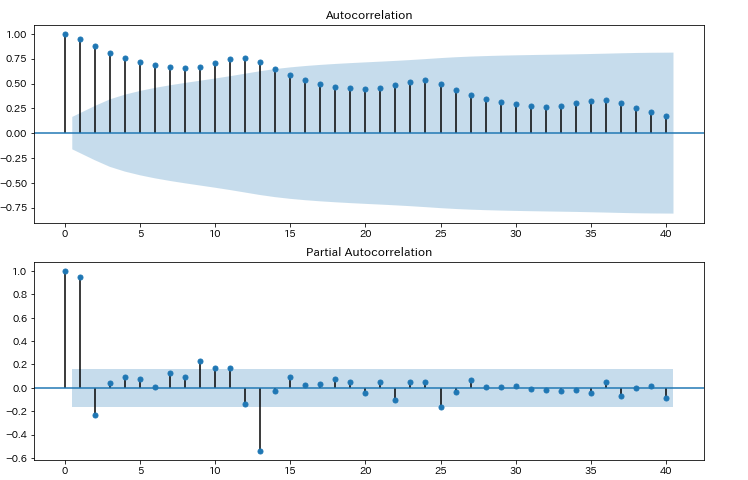
上のグラフは「自己相関」下のグラフは「偏自己相関」のグラフです。水色の領域は、「自己相関係数が0である」という帰無仮説の95%信頼区間です。この領域の外は統計的に有意差がある、ということになります。
diffをとって、同じように「自己相関」「偏自己相関」のグラフを描いてみましょう。
# 自己相関のグラフ
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(diff, lags=40, ax=ax1)
# 偏自己相関のグラフ
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(diff, lags=40, ax=ax2,method='ywmle')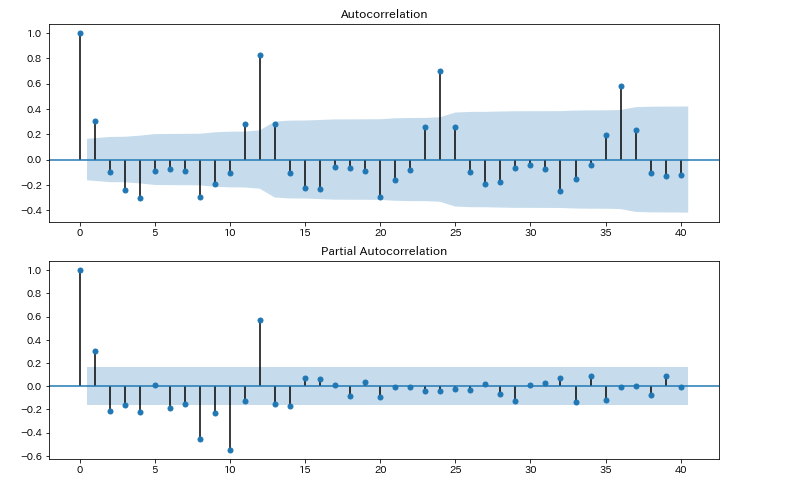
ラグ12、つまり12か月のところで強い相関がみられます。12か月周期がありそうです。
モデルの構築
いよいよモデルの構築です。ここでは、ARモデルとSARIMAモデルを扱ってみます。ARモデルは、時間の変化に対し規則的に値が変化するモデルでした。一方、SARIMAは、ARIMAモデルに季節周期を考慮したものです。
ARモデル
今回、扱うARモデルや、その他、MAモデル、その組み合わせであるARMAモデルは、データが「定常過程」であることが前提となります。つまり、ARモデル、MAモデル、ARMAモデルでは「非定常」なデータをそのままでは扱うことができません。
このような場合には、「定常なデータ」に加工してから扱うのでしたね。現系列にはトレンドがあったので、差分データでモデルを構築しましょう。作成したモデルの適切さを判断するためには、残差分析が必要です。ARモデルにおける残差は平均0の正規分布に従い、残差の間には相関がないことが期待されます。
# ARで予測
predict=ar.predict('1959-12-01','1961-12-01')
plt.figure(figsize=(16,8))
plt.plot(diff[diff.index.year>1958])
plt.plot(predict,'r')
plt.title('ARモデルによる予測',fontsize=20)
plt.grid()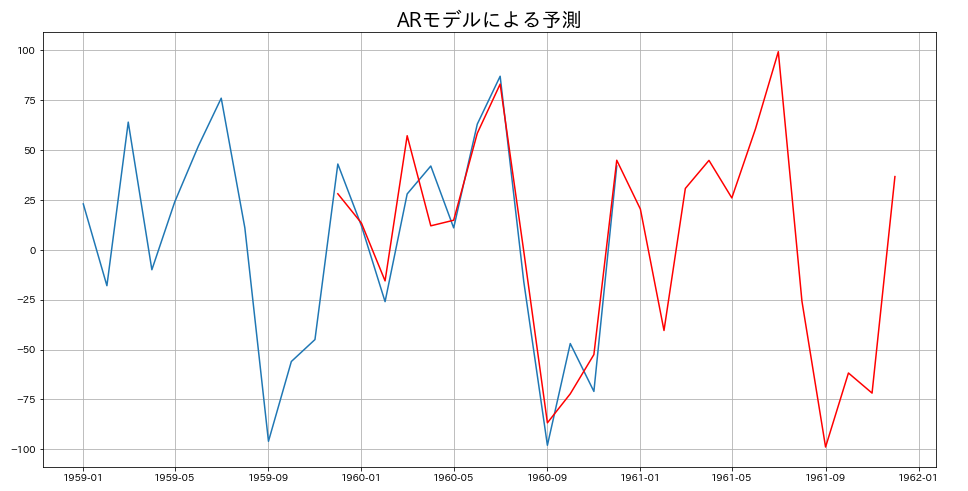
SARIMAモデル
次に、SARIMAモデルで予測してみましょう。SARIMAモデルは、季節調整済みのARIMAモデルでしたね。また、ARIMAモデルは、ARMAの発展形で差分も一緒も扱えるからトレンドをもったデータにも適用できます。ただ、ARIMAモデルは季節変動があると上手くモデルに適用できないけど、SARIMAは季節性のある時系列データも扱えるようになっている、という特徴があります。
早速、モデル構築をしていきましょう。SARIMAモデルはp,q,d,P,Q,D,sのパラメータがありました。sは周期のパラメータで、先におこなったdiffの自己相関、偏自己相関のグラフから12か月の周期がありそう、と結論付けました。
その他のパラメータに関しては、ある程度あたりをつけて(どのくらいの値になるかの範囲の目安をつけて)、すべての組み合わせを試してAICで決める、といった方法がとられます。
このあたりを付けるにあたっては目安があり、
のようです。パラメータの決め方については別途扱うとして、ここでは、(p,q,d)=(2,1,2),(P,Q,D,s)=(1,1,1,12)としてモデルを構築してみることにします。
# Series型にする
ts=data.passengers
# trainデータを取り出す
ss=ts[ts.index.year<=1959]
# ライブラリのインポート
from statsmodels.tsa.statespace.sarimax import SARIMAX
# モデルの構築
sarima=SARIMAX(ss,order=(2,1,2),seasonal_order=(1,1,1,12)).fit()
# モデルによる予測とプロット
predict=sarima.predict('1959-12-01','1961-12-01')
predict_dy=sarima.get_prediction('1959-12-01','1961-12-01')
predict_dy_ci=predict_dy.conf_int(alpha=0.05)
plt.figure(figsize=(16,8))
plt.plot(ts[ts.index.year>1958])
plt.plot(predict,'r')
plt.fill_between(predict_dy_ci.index,
predict_dy_ci.iloc[:,0],
predict_dy_ci.iloc[:,1],
color='gray',
alpha=0.2)
plt.title('SARIMAモデルによる予測',fontsize=20)
plt.grid()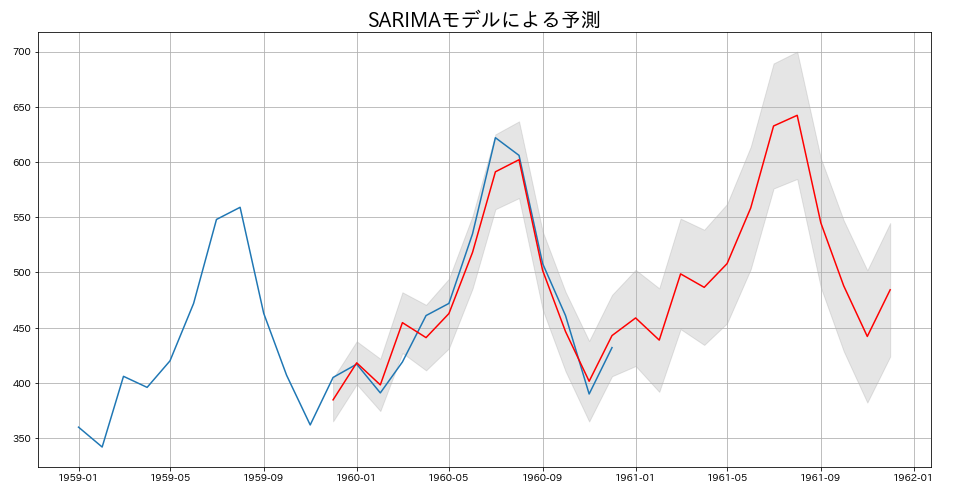
まとめ
いかがでしたか?今回はARモデルとSARIMAモデルで、実際にモデルを構築して予測をしてみました。ARモデルは自己回帰モデルの基本的な形、SARIMAモデルは、季節周期を含むARIMAモデルでしたね。SARIMAモデルでは、決めなければいけないパラメータが多く大変ですが、今回の記事の中ではその部分を省略して、パラメータが決まっているものとして、モデルの構築・予測を行いました。実際のパラメータは、総当たりで組み合わせを試すなどの力技も必要となってきます。この辺は、別の投稿で扱うことにします。
▶ データ分析を基本から学びたい方は、以下の記事も参考にしてください。



コメント