統計学：諸学者向けにPythonで$chi^{2}$値と期待度数を求める方法を基本から解説

この記事はこんな方におススメです

データを分析をしたいが、どこから始めてよいかわからない方
データを仕事に活かしたいが、データの解釈の仕方がわからない方
統計学を体系的に学んだことがない、初学者の方

はじめに
$\chi^{2}$値と期待度数
まとめ

はじめに

統計学を学んだことがない方を対象に基本から解説しています。今回は、「$\chi^{2}値と期待度数$」をPythonで求める方法を基本から解説します。「 $\chi^{2}値 $」は、観測度数が期待度数がどのくらい離れているかを表すものでした。期待度数と離れているということは、カテゴリ変数間の関係が強いことを意味します。但し、標準化された値ではないのでそのまま利用することはできなかったのでしたね。

▶ $\chi^{2}$値や期待度数について学びたい方は以下の投稿を先にご覧ください。

統計学：初学者向けに連関係数について基本から解説します

今回は、「連関係数」を基本から解説します。連続する変数間の相関関係の強さを表す「相関係数」に対して、カテゴリ変数間の相関関係の強さを表す「連関係数」というものがあります。カテゴリ変数間の関係を調査する際には、「分割表」を扱うことが多いので、あわせて基本から解説します。

$\chi^{2}$値と期待度数

サンプルデータ

今回は、seabornで用意されている学習用のデータセットを使うことにしましょう。「taxis」というデータセットを使うことにしましょう。以下のコードでデータを読み込んでください。

# ライブラリのインポート
import pandas as pd
import seaborn as sns
from scipy import stats

# データセットの読み込み
df_taxis=sns.load_dataset('taxis')
df_taxis.head()

すると、次のようなデータフレームが作成されます。

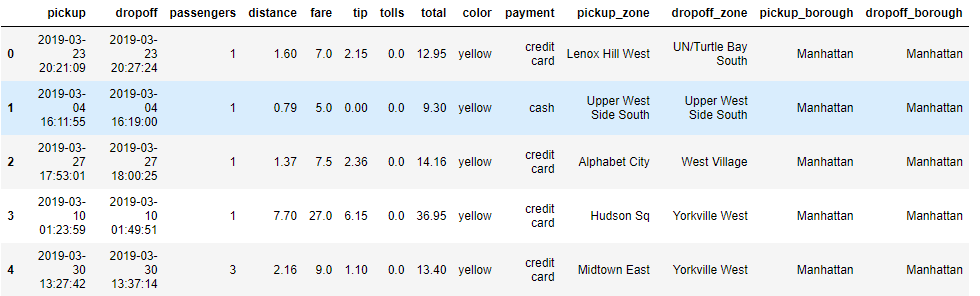
タクシーの乗車・降車時刻、乗車人数、距離、運賃、チップ・・・etcのデータがありますね。データの要約情報をみてみましょう。

# データフレームの要約情報
df_taxis.info()

Dtypeがobjectとなっているのが、このデータフレーム内でカテゴリ変数として扱われているものです。今回はcolorとpaymentを使って $\chi^{2}$値と期待度数を求めてみましょう。

クロス集計

まず、colorとpaymentでクロス集計をしてみましょう。pandasにはcrosstabというクロス集計用のメソッドが用意されています。これは、次のように使います。

pd.crosstab(xarray, yarray)

xaarrayの部分が行方向（index）になるデータ、yarrayが列方向（columns）になるデータです。さっそくやってみましょう。

# クロス集計
cont_table=pd.crosstab(df_taxis['color'],df_taxis['payment'])
cont_table

簡単ですね。colorはタクシーの色でしょうか？（よくわからずすみません）緑と黄いろがあります。paymentは支払方法ですね。現金とクレジットカードがあります。これらでクロス集計した結果が得られます。これはデータセットを集計したものですが、仮に、colorとpaymentに相関がない場合はどうであったか？というのが期待度数です。これを求めてみましょう。

$\chi^{2}$値と期待度数

$\chi^{2}$値と期待度数を求めるにはstatsモジュールを利用します。引数にデータのクロス集計を放り込むだけで、 $\chi^{2}$値、p値、自由度、期待度数を一発で算出してくれます。3つの値と、期待度数がarray形式ではいったタプルが戻ります。

やってみましょう。

# χ乗値と期待度数の算出
stats.chi2_contingency(cont_table, correction=False)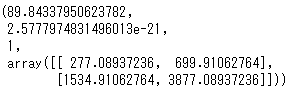

このように3つの値とarrayが返ってきてますね。一つの目の値が$\chi^{2}$値、arrayが期待度数になります。このように返り値が複数ある場合は変数に入れてしまったほうがわかりやすいですね。

# χ乗値と期待度数の算出
chi2, p, dof, expected=stats.chi2_contingency(cont_table, correction=False)
print('χ2乗値は',chi2)
print('期待度数は\n',expected)

chi2_contingencyは検定をおこなう関数で、引数correction=Falseは、「離散型分布を連続型分布（カイ二乗分布や正規分布）に近似させて統計的検定する設定」をおこないます。ここではこの補正をしない（False）設定としています。

さて、先ほどのクロス集計表と期待度数を比較するとどうでしょうか？

cashのときのcolorの比が、期待度数では1534.9/277.0=5.54であるのに対し、クロス集計では1412/400=3.53となっています。なんだか連関がありそうですね。

まとめ

今回は、$\chi^{2}$値と期待度数をPythonで求める方法を解説しました。statsモジュールのchi2_contingencyを使えば一発でしたね。ちなみに戻り値が複数ある場合は、「Shift ＋Tab」とすると、調べることができます。chi2_contingency()ではReturnsは以下のように期待されています。