- データを分析をしたいが、どこから始めてよいかわからない方
- データを仕事に活かしたいが、データの解釈の仕方がわからない方
- 統計学を体系的に学んだことがない、初学者の方
▶ 初学者向けに統計学を基本から解説しています。こちらの記事もご参考にどうぞ。
はじめに
統計学を学んだことがない初学者を対象にして、基本から解説しています。今回はPythonで「連関の検定」する方法を基本から解説していきます。前回、カイ二乗値を検定統計量としてこれらが得られる確率によって帰無仮説を棄却できるかどうかを判断する、と解説しました。今回はPythonを使って実際に検定をする方法を基本から解説します。
連関の検定
準備
比率差の検定には、scipyライブラリのstatsモジュールにあるshi2_contingency()メソッドを用います。はじめにこの使い方をまとめておきましょう。
contingencyは分割表のことでしたね。引数のobsは観測度数、correctionはイェイツの修正*1です。イェイツの修正に関してはウィキペディアに以下のような説明があります。
統計学において, イェイツの修正 (またはイェイツのカイ二乗検定)は分割表において独立性を検定する際にしばしば用いられる。場合によってはイェイツの修正は補正を行いすぎることがあり、現在は用途は限られたものになっている。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
利用するケースもあるようですが、「不幸なことに、イェイツの修正は修正しすぎる傾向があり、このことは全体として控えめな結果となり帰無仮説を棄却すべき時に棄却し損なってしまうことになりえる(第2種の過誤)。」というような説明もあり、基本的にはFalseで使って問題ないかと思います。
ちなみに引数や戻り値は完璧に覚えておく必要はありません。以下のようにメソッド名を入力した状態で「Shift + Tab」をするとツールチップを表示してくれます。
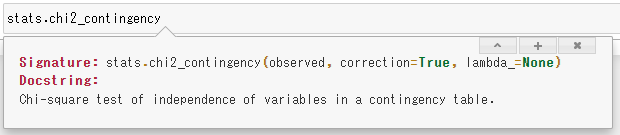
これをみると、すぐにどんな引数があるのかわかりますね。さらに右上の「^」や「+」をクリックすることで、詳しい情報をみることができます。
<「^」をクリックしたとき>
ブラウザの領域が分割され、下の領域にさらに詳しい情報が表示されます。parametersに引数、Returnsに返り値の情報など様々情報が載っています。
※「+」をクリックした場合はポップアップ形式で表示されます。
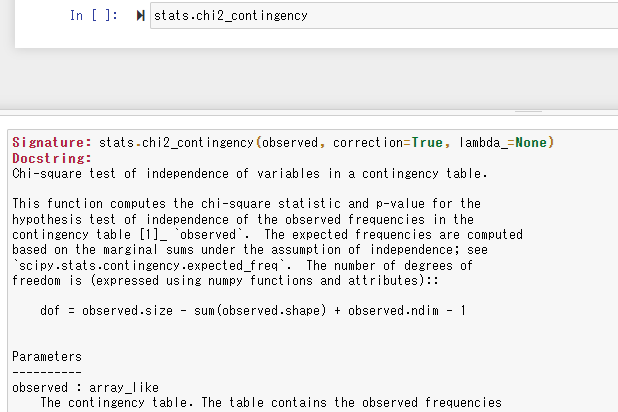
返り値の部分を見ると、以下のように4つの値が返ってくるのがわかります。

「chi2」はカイ二乗値ですね。「p」はp値。カイ二乗分布から、観測地から計算したカイ二乗値が得られる確率でしたね。「dof」は「Degrees of freedom」と書いてあります。これが自由度となります。最後の「expected」は期待度数です。なので、初めからこれを次のように変数に入れるとわかりやすいですね。
Pythonによる連関の検定
次のようなケースを考えてみることにしましょう。1000人にメールを配信したときに、メールの受信者が「製造業であるか否か」によって「メールを開いたかどうか」を集計したときに以下が得られたとします。

このとき「製造業」であるか否かとメールを「開封」したかどうかに連関があるかどうかを検定してみましょう。帰無仮説、対立仮説は次のようになります。
- 帰無仮説:「製造業」と「開封」には連関がない
- 対立仮説:「製造業」と「開封」には連関がある
早速やってみましょう。
# ライブラリのインポート
import pandas as pd
from scipy import stats
import seaborn as sns
# メール配信結果
mail_df=pd.DataFrame(
[[432,418],[78,72]],
index=['製造業','製造業でない'],
columns=['メールを開いた','メールを開かなかった'])
# 連関の検定
stats.chi2_contingency(mail_df,correction=False)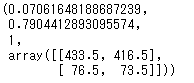
たった1行で検定ができるのは驚きですね。結果を見ると、カイ二乗値が0.07、p値が0.79, 自由度が1で、最後にarrayで期待度数が返ってきています。有意水準を5%としたときにp値は0.79(>0.05)なので帰無仮説は棄却されない、という結果となりました。
ちなみに今回は、chi2_contingency()の第一引数にクロス集計した形のデータフレームを指定しましたが、次のように二十リストにして渡しても同じ結果を得ることができます。一応、試しておきましょう。
# 連関の検定(二重リスト)
stats.chi2_contingency([[432,418],[78,72]],correction=False)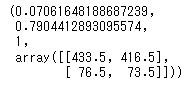
このように全く同じ結果を得ることができます。
まとめ
今回はPythonで連関の検定をする方法を扱いました。たった一行で連関の検定を
することができます。統計ツールは偉大ですね。ただ、内容を分からずに使う、ということの内容に背景にある理論の概要もつかむようにしておきましょう。



コメント